Figure shows two discs of same mass m. They are rigidy attached to a spring of stiffness k. The system is in equlibrium. From this equilibrium position, the upper disc is pressed down slowly by a distance x and released. Find the minimum value of x, if the lower disc is just lifted off the ground.
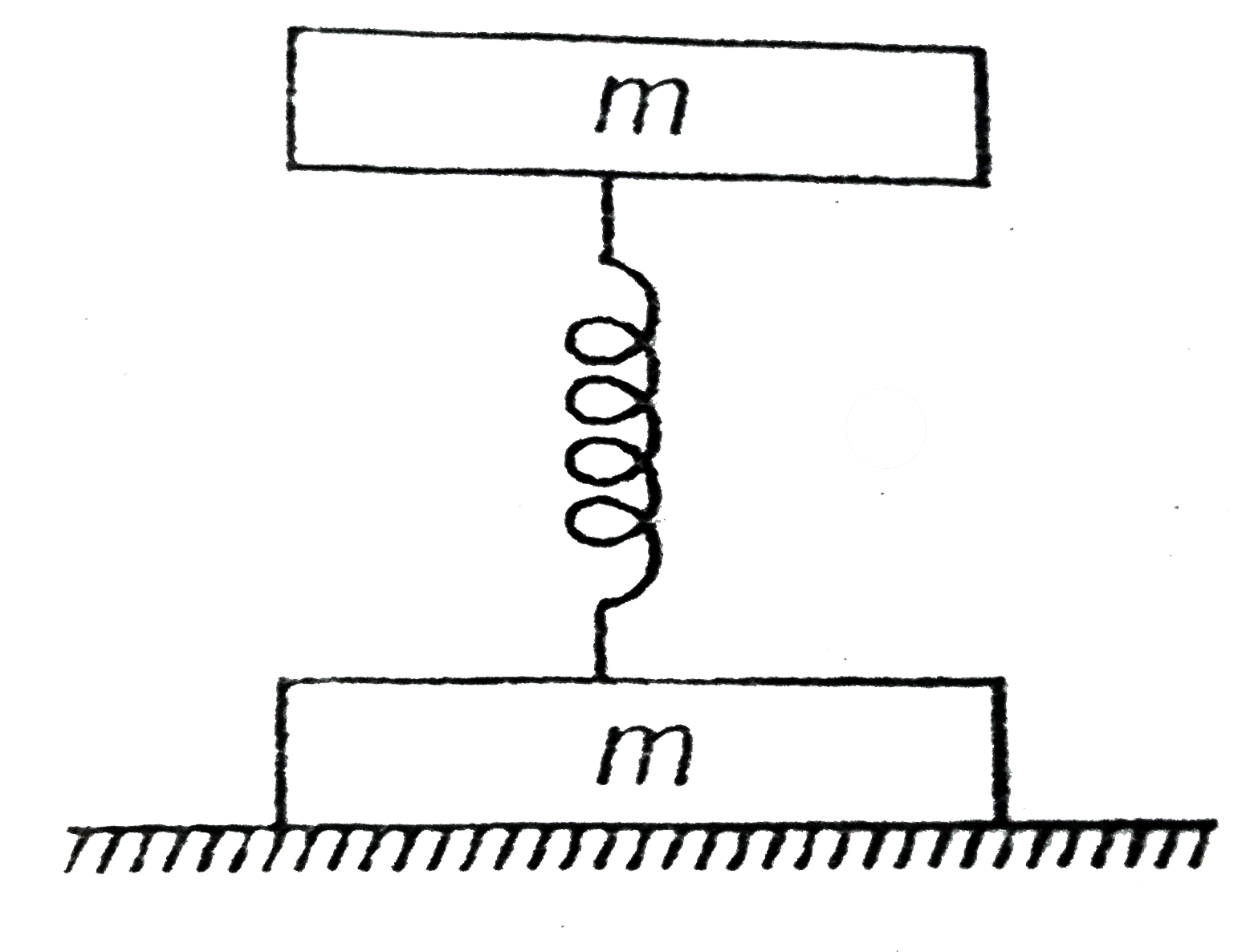
Let us first find out the minimum elongation (x') needed to lift the lower discc from the ground . THe free body digram of the lower disct at this instant will be
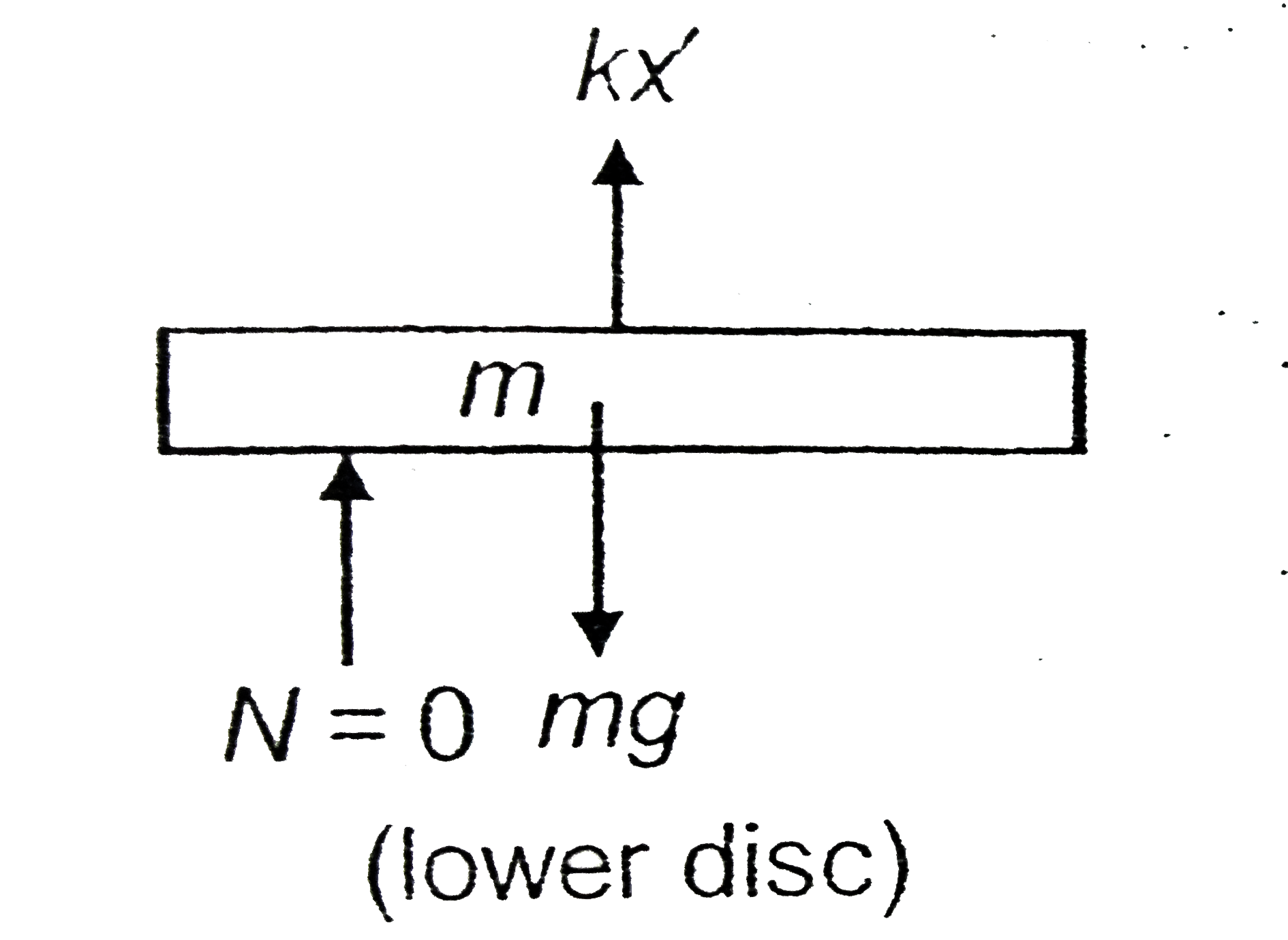
The system given in the question is in equlibrium thus for the equlibrium of upper disc initial compression (x0) in spring is
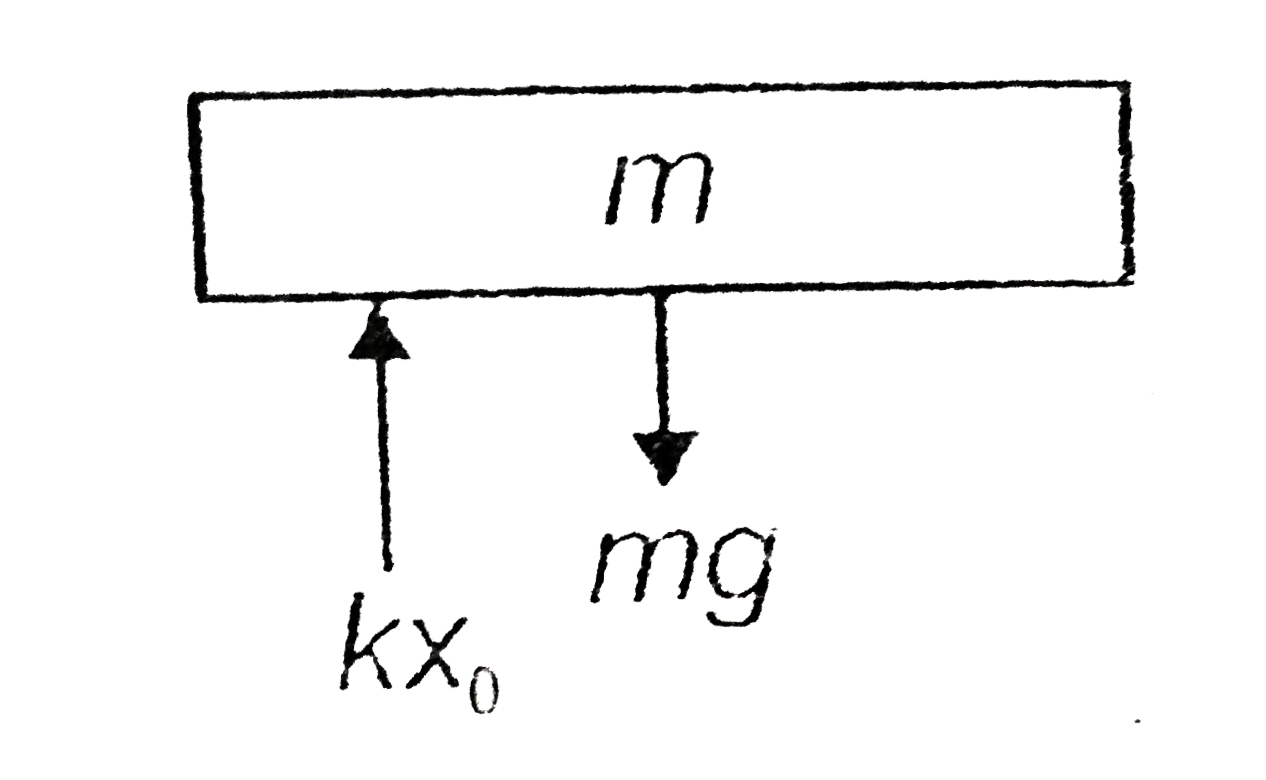
now from this equlibrium state spring is further compressed by an amount x and released. Now let us apply energy conservation from this compressed state and final state. Let us take the reference for gravitation potential energy at unstreatched position then
12k(x+x0)2=−mg(x+x0)=12kx2+mgx'
Now, x0=mgk
x=mgk
on solving, we get
x=2mgk
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION
2 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF
95 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A disc of mass 3 m and a disc of mass m are connected by a massless spring of stiffness k. The heavier disc is placed on the ground with the spring vertical and lighter disc on top from its equilibrium position the upper disc is pushed down by a distance δ and released. Then.
View SolutionA disc of mass m hanged by a string is attached at P and a spring of stiffness k is attached at Q. Find the frequency of small angular oscillation of the disc if the string does not slide over the pulley. Assume l0=Ml of the dise about O.

View SolutionA sand bag of mass m is hanging from a light spring of stiffness k. Find the elongation of the spring. If we pull the sand bag down by an additional distance x and release it, find its acceleration and maximum velocity of block.

View SolutionIn the figure, a block of mass m is rigidly attached to two identical springs of stiffness k each. The other ends of the springs are connected to the fixed wall. When the block is in equilibrium, length of each spring is b, which is greater than the natural length of the spring. The time period of the oscillation of the block if it is displaced by small distance perpendicular to the length of the springs and released. Space is gravity free.
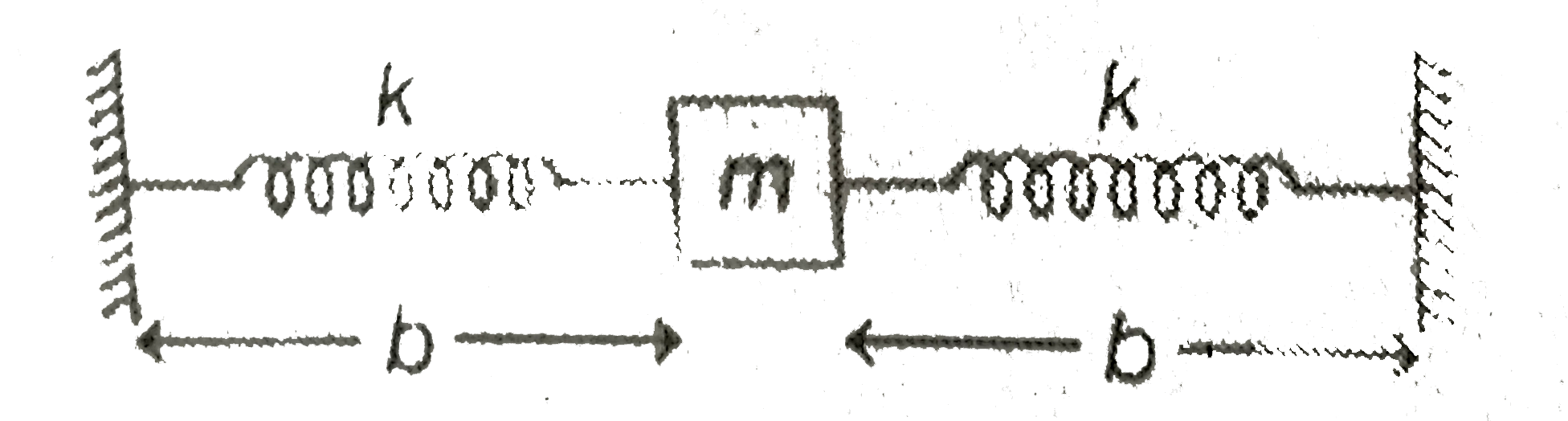
View SolutionPassage VIII A disc of mass m and radius R is attached with a spring of force contant k at its center as shown in figure. At x-0, spring is unstretched. The disc is moved to x=A and then released. There is no slipping between disc and ground. Let f be the force of friction on the disc from the ground.

f versus t (time) graph will be as
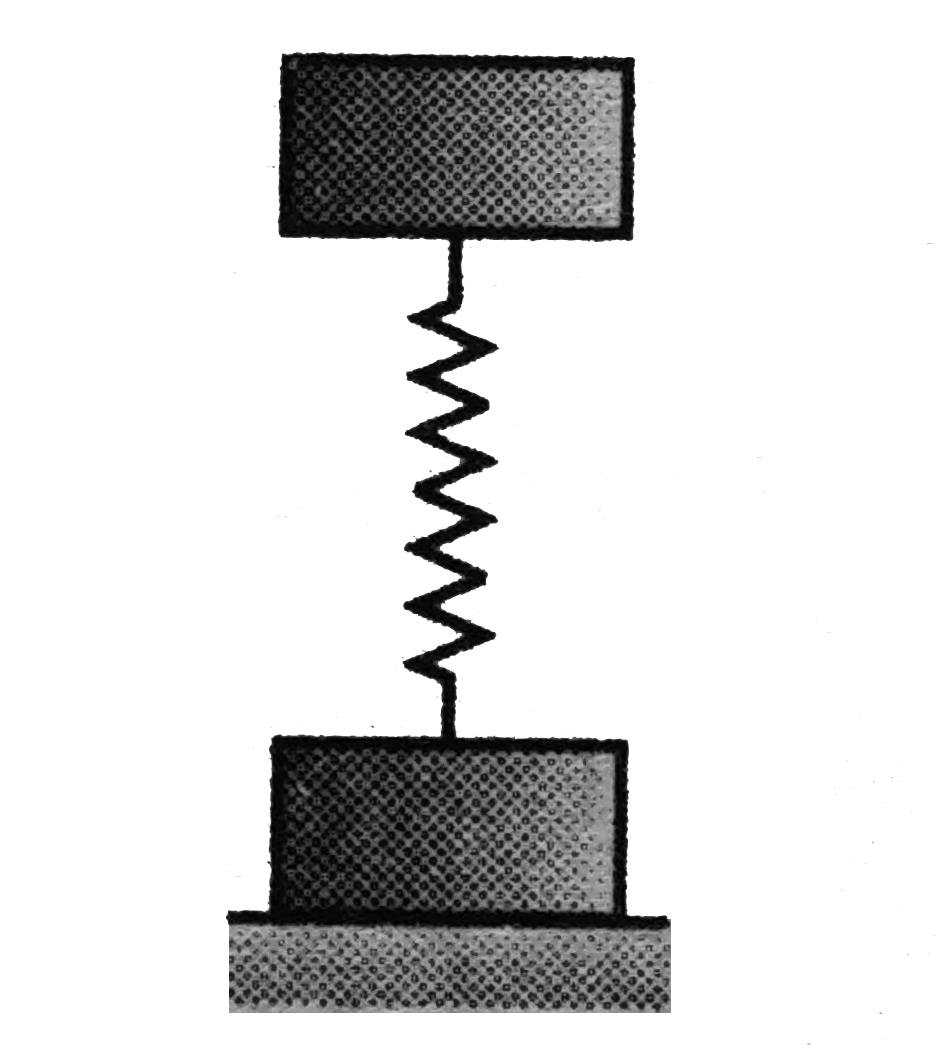
View SolutionIn the figure shown, a block A of mass m is rigidy attached to a light spring of stiffness k and suspended from a fixed support. Another block B of same mass is just placed on it and blocks are in equilibrium. Suddenly the block B is removed. Choose the correct options (s) afterward.
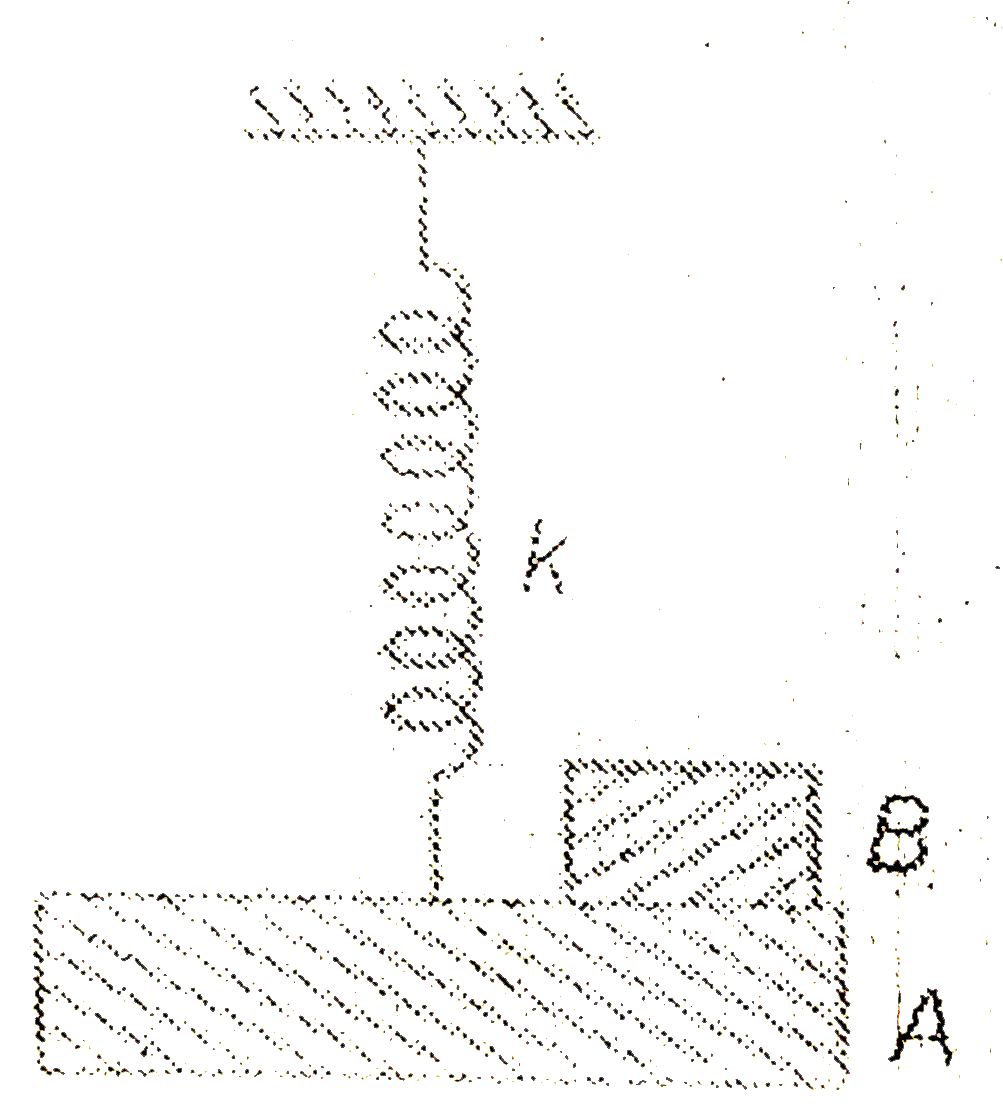
View SolutionTwo discs, each having mass m, are attached rigidly to the ends of a vertical spring. One of the discs rests on a horizontal surface and the other produces a compression x0 on the spring when it is in equilibrium. How much further must the spring be compressed so that when the force causing compression is removed, the extension of the spring will be able to lift the lower disc off the table?
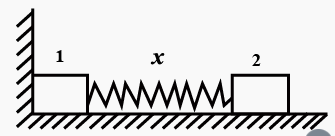
View SolutionTwo blocks of masses m1 and m2, connected by a weightless spring of stiffness k rest on a smooth horizontal plane as shown in Fig. Block 2 is shifted a small distance x to the left and then released. Find the velocity of centre of mass of the system after block 1 breaks off the wall.

View SolutionTwo bars of masses m1 and m2 connected by a weightless spring of stiffness k, rest on a smooth horizontal plane. Bar 2 is shifted by a small distance x0 to the left and released. The veloicyt of the centre of mass of the system when bar 1 breaks off the wall is
View SolutionA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.

View Solution
