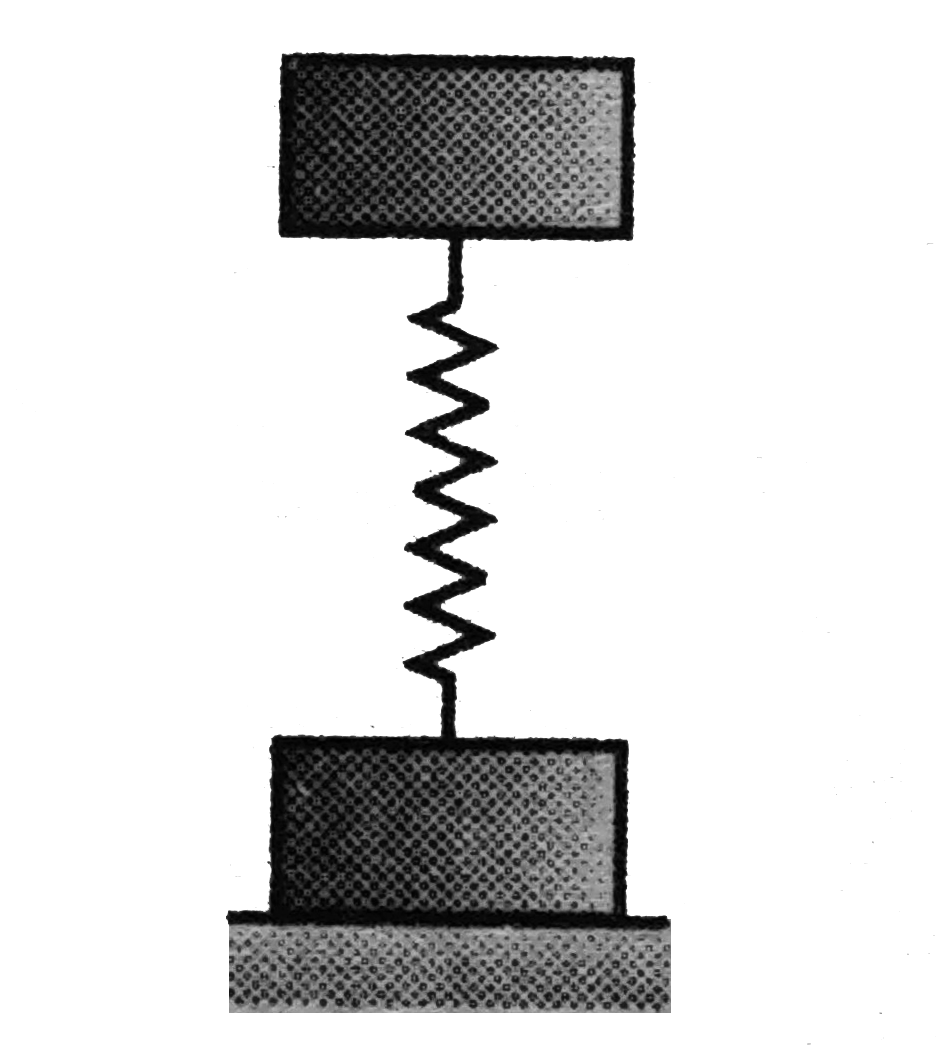
Two discs, each having mass m, are attached rigidly to the ends of a vertical spring. One of the discs rests on a horizontal surface and the other produces a compression x0 on the spring when it is in equilibrium. How much further must the spring be compressed so that when the force causing compression is removed, the extension of the spring will be able to lift the lower disc off the table?
(a) x0
(b) 2x0
(c) 3x0
(d) 1.5x0
The correct Answer is:B
A is the position of the spring when it is in its normal uncompressed length. The upper disc compresses the spring by x0 when spring is in equilibrium. So kx0=mg. Hence, B is the equilibrium position of the spring. Let it be further compressed by y and released. After releasing it can be proved that the spring will go up to the position D so that BC=BD. Extension in the spring at this position
=y−x0.
Now for lifting up of the lowe disc:
k(y−x0)=mg⇒y=mgk+x0
⇒y=x0+x0=2x0

Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Multiple Correct
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Linked Comprehension
Explore 55 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Subjective
Explore 23 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
"A mass is attached to one end of a spring and by holding the other end in hand, the spring is whirled in a horizontal circle" What happens to the length of the spring ?
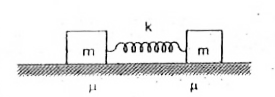
View SolutionTwo blocks each having mass m is attached to each other with a spring having force constant k. The system is placed on a rough horizontal surface having coefficient of friction μ. The maximum initial compression, that can be given to the spring so that when released the blocks do not move is
View SolutionThe spring is compressed by a distance a and released. The block again comes to rest when the spring is elongated by a distance b. During this
View SolutionA 16kg block moving on a frictionless horizontal surface with a velocity of 4m/s compresses an ideal spring and comes to rest. If the force constant of the spring be 100N/m, then how much is the spring commpressed ?
View SolutionAll surfaces shown in figure are smooth system is released with the spring unstretched In equilibrium, compression in the spring will be

View SolutionAll surfaces shown in figure are smooth system is released with the spring unstretched In equilibrium, compression in the spring will be

View SolutionTwo masses m and 2m are attached to two ends of an ideal spring as shown in figure. When the spring is in the compressed state, the energy of the spring is 60 J, if the spring is released, then at its natural length

View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

View SolutionA block of mass m is suddenly released from the top of a spring of stiffness constant k.
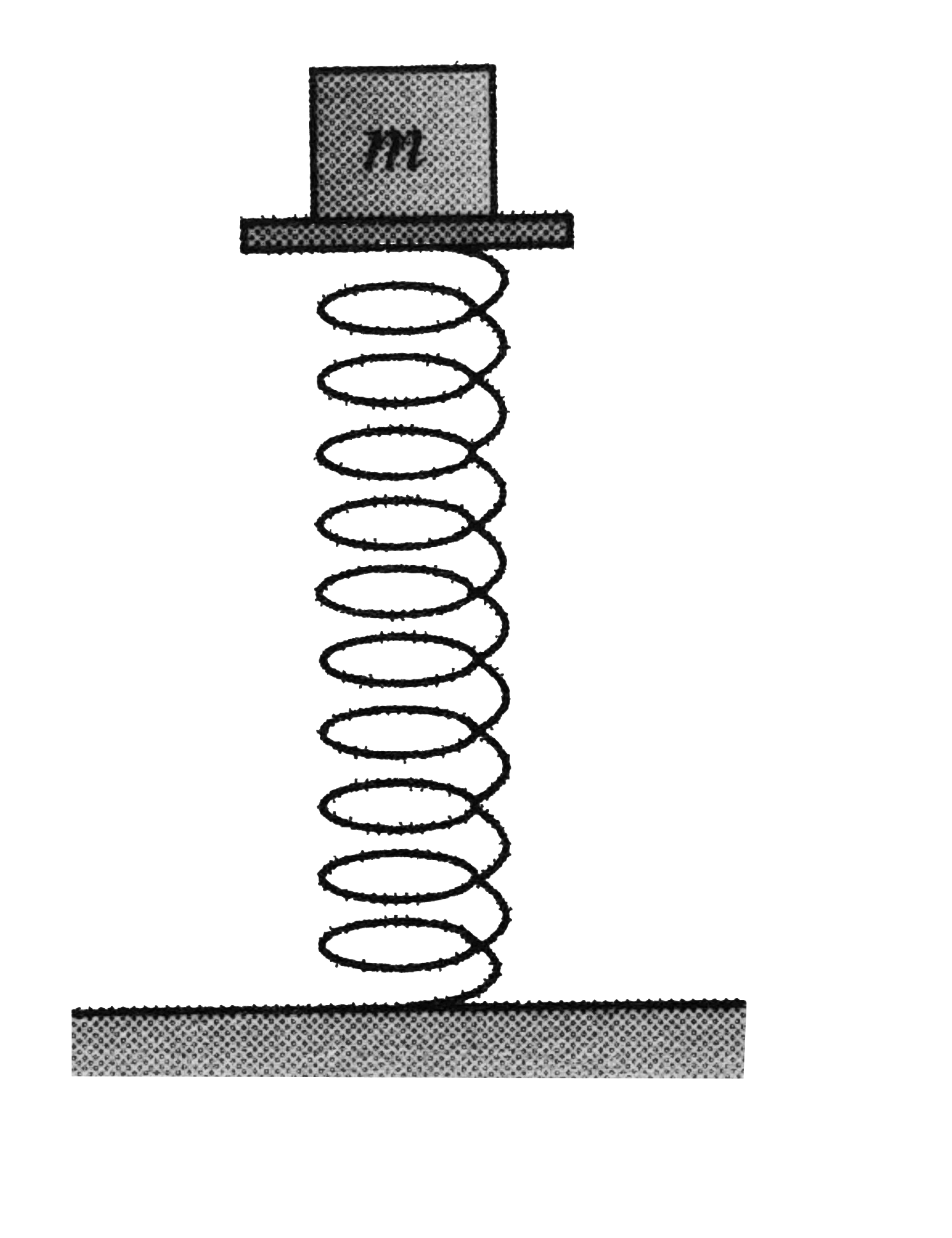
a. Find the acceleration of block just after release.
b. What is the compression in the spring at equilibrium.
c. What is the maximum compression in the spring.
d. Find the acceleration of block at maximum compression in the spring.
View SolutionA vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring , so that the spring is compressed by a distance d. The net work done in the process is
View Solution

