The potential energy function associated with the force →F=4xyˆi+2x2ˆj is
(a) U=−2x2y
(b) U=−2x2y+constant
(c) U=2x2y+constant
(d) Not defined
The correct Answer is:B
To find the potential energy function associated with the force vector →F=4xy^i+2x2^j, we need to follow these steps:
Step 1: Understand the relationship between force and potential energy
The potential energy U is related to the force →F by the equation:
→F=−∇U
This means that the force is the negative gradient of the potential energy function. In Cartesian coordinates, this can be expressed as:
→F=−(∂U∂x^i+∂U∂y^j)
Step 2: Write down the components of the force
From the given force vector:
→F=4xy^i+2x2^j
we can identify the components:
Fx=4xyandFy=2x2
Step 3: Set up the equations for potential energy
Using the relationship between force and potential energy, we have:
−∂U∂x=4xy(1)
−∂U∂y=2x2(2)
Step 4: Integrate the first equation
From equation (1):
∂U∂x=−4xy
Integrating with respect to x:
U=−4xy2+g(y)
where g(y) is an arbitrary function of y.
Step 5: Differentiate with respect to y and use the second equation
Now we differentiate U with respect to y:
∂U∂y=−8xy+g′(y)
Setting this equal to equation (2):
−8xy+g′(y)=−2x2
Rearranging gives:
g′(y)=−2x2+8xy
Step 6: Solve for g(y)
Since g′(y) must not depend on x, we can set the coefficient of x to zero:
8y=0⟹y=0(not useful)
Thus, we can assume g(y) is a function of y alone. Integrating g′(y) gives:
g(y)=−2y2+C
where C is a constant of integration.
Step 7: Combine results to find the potential energy function
Now substituting g(y) back into our expression for U:
U=−4xy2−2y2+C
Final Result
Thus, the potential energy function associated with the force →F is:
U(x,y)=−4xy2−2y2+C
The potential energy U is related to the force →F by the equation:
→F=−∇U
This means that the force is the negative gradient of the potential energy function. In Cartesian coordinates, this can be expressed as:
→F=−(∂U∂x^i+∂U∂y^j)
From the given force vector:
→F=4xy^i+2x2^j
we can identify the components:
Fx=4xyandFy=2x2
Using the relationship between force and potential energy, we have:
−∂U∂x=4xy(1)
−∂U∂y=2x2(2)
From equation (1):
∂U∂x=−4xy
Integrating with respect to x:
U=−4xy2+g(y)
where g(y) is an arbitrary function of y.
Now we differentiate U with respect to y:
∂U∂y=−8xy+g′(y)
Setting this equal to equation (2):
−8xy+g′(y)=−2x2
Rearranging gives:
g′(y)=−2x2+8xy
Since g′(y) must not depend on x, we can set the coefficient of x to zero:
8y=0⟹y=0(not useful)
Thus, we can assume g(y) is a function of y alone. Integrating g′(y) gives:
g(y)=−2y2+C
where C is a constant of integration.
Now substituting g(y) back into our expression for U:
U=−4xy2−2y2+C
Thus, the potential energy function associated with the force →F is:
U(x,y)=−4xy2−2y2+C
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Multiple Correct
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Linked Comprehension
Explore 55 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Subjective
Explore 23 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
A single conservative force acting on a particle varies as →F=(−Ax+Bx2)ˆiN, where A and B are constants and x is in meters. (a) Calculate the potential energy function U(x) associated with this force, taking U=0 at x=0. (b) Find the change in potential energy and the change in kinetic energy of the system as the particles moves from x=2.00m to x=3.00m.
View SolutionA conservative force acts on a particle as the particle moves along the positive x-axis from origin origin to x=2m. The force is parallel to x-axis. Now, consider four different cases, as shown in the figures, 1, 2, 3, and 4, where the forces is shown as a function of x. Rank the situations according to the change in potential energy associated with the force, least ( or most negative) to greatest ( or most positive).
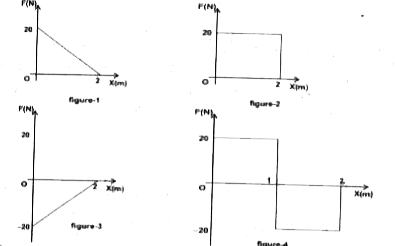
View Solution
Knowledge Check
Assertion: Work done by friction over a closed path is not zero and no potential energy can be associated with friction.
Reason: Every force encountered in mechanics have an associated potential energy.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true not but reason is not the correct explanation of assertion.CIf assertion is true but reason is falseDIf both assertion and reason are false.
The potential energy function for the force between two in a diatomic molecule can approximately be expressed as U(x)=ax12−bx4, where a and b are positive constants, and x is the distance between the atoms. Answer the following question by selecting most appropriate alternative.
The graph between potential energy vs x will be
View SolutionA potential energy function for a two-dimensional force is the form U=3x2y−7x. Find the force that acts at the point (x,y).
View SolutionThe potential energy function of a particle in the x-y plane is given by U=k(x+y), where (k) is a constant. The work done by the conservative force in moving a particlae from (1,1) to (2,3) is .
View SolutionThe potential energy (in joules ) function of a particle in a region of space is given as:
U=(2x2+3y2+2x)
Here x,y and z are in metres. Find the maginitude of x compenent of force ( in newton) acting on the particle at point P ( 1m, 2m, 3m).
View SolutionAssertion: Frictional forces are conservative forces.
Reason: Potential energy can be associated with frictional forces.
View SolutionPotential energy function along x−axis in a certain force field is given as
U(x)=x44−2x2+112x2−6x
For the given force field :−
(i)the points of equilibrium are x=1, x=2 and x=3
(ii) the point x=2 is a point of unstable equilibrium.
(iii) the points x=1 and x=3 are points of stable equilibrium.
(iv) there exists no point of neutral equilibrium. The correct option is :−
View SolutionA particle moves 5m in the +x direction while being acted upon by a constant force→F=(4N)ˆi+(2N)ˆj−(4N)ˆk . The work done on the particle by this force is
View Solution

