Consider a non conduting ring of radius r and mass m and a particle of same mass, both at rest in free space. The particle is on the axis of the ring and far away from the ring. An amount Q of positive charge is uniformly distributed on the ring and the particle is given a positive charge q. The particle is imparted a velocity v towards the centre of the ring. Consider the consequences given in the columns and answer the following question
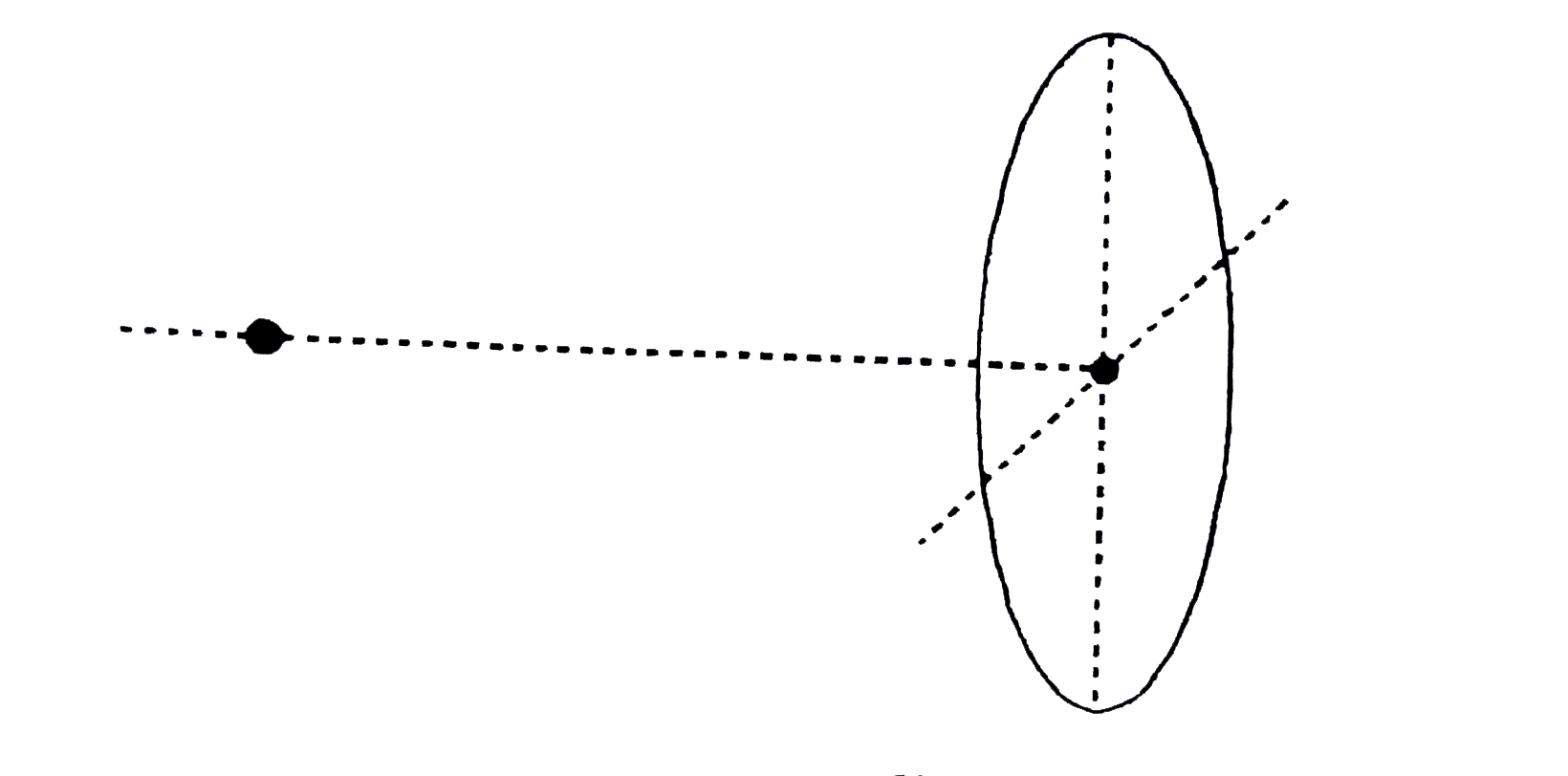
Which of following options is the correct is the representation if
The correct Answer is:B
Let v be the velocity of particle for which both moves together finally
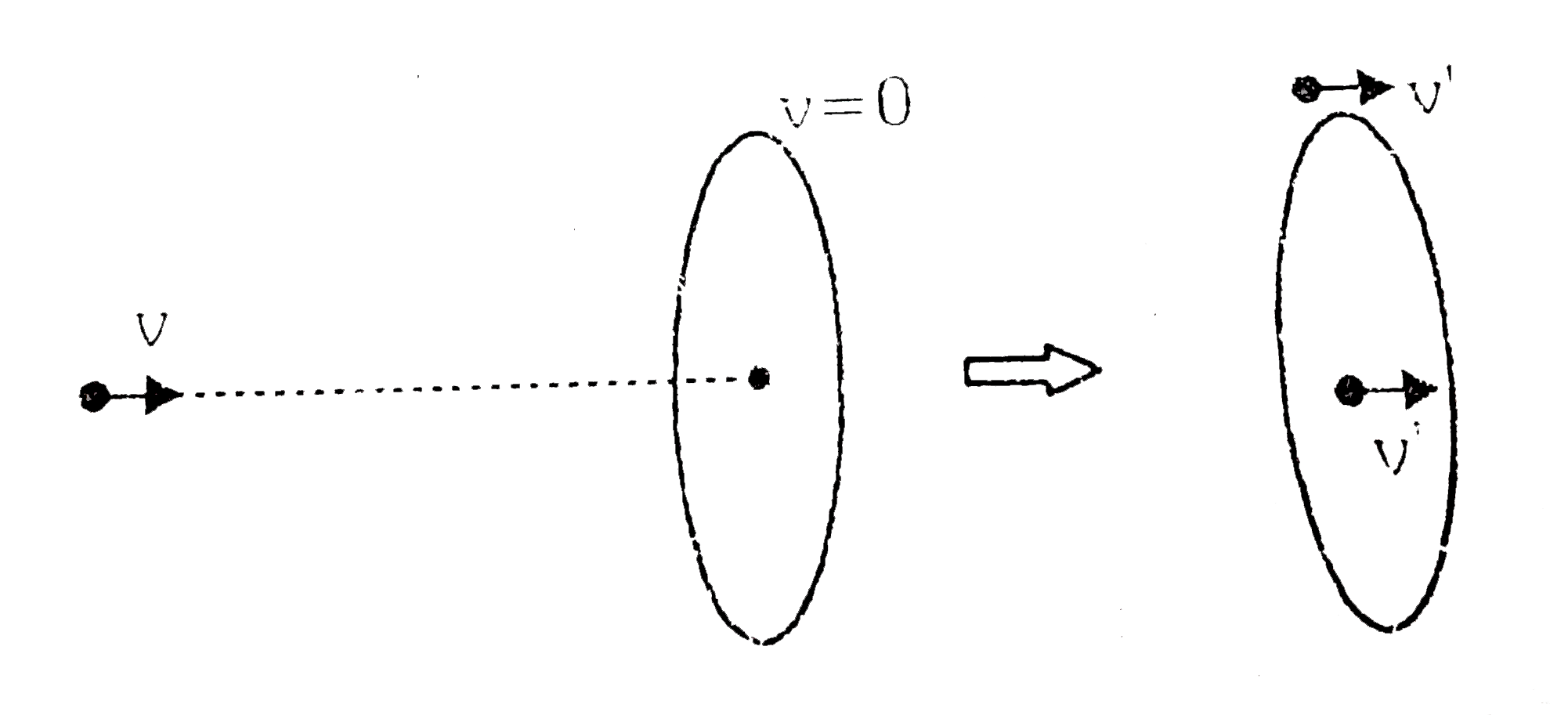
If then velocity of particle continously decrease and that of ring continously increase. Final velocity of particle becomes zero and that of ring becomes v
If then particle crosses the ring and again it's velocity start increasing and finally becomes v and that of ring becomes zero.
Minimum speed of particle
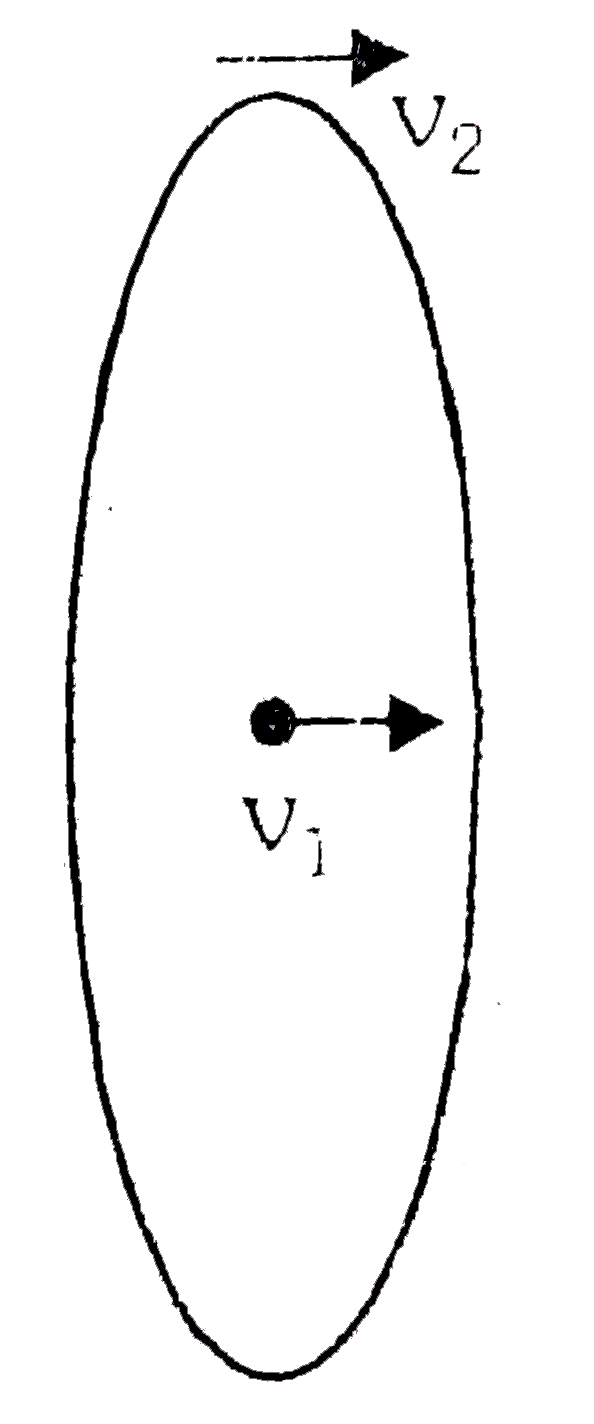
Maximum speed of ring
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physic
48 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS
17 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - Part-1 Physics
15 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
Consider a non conduting ring of radius r and mass m and a particle of same mass, both at rest in free space. The particle is on the axis of the ring and far away from the ring. An amount Q of positive charge is uniformly distributed on the ring and the particle is given a positive charge q. The particle is imparted a velocity v towards the centre of the ring. Consider the consequences given in the columns and answer the following question
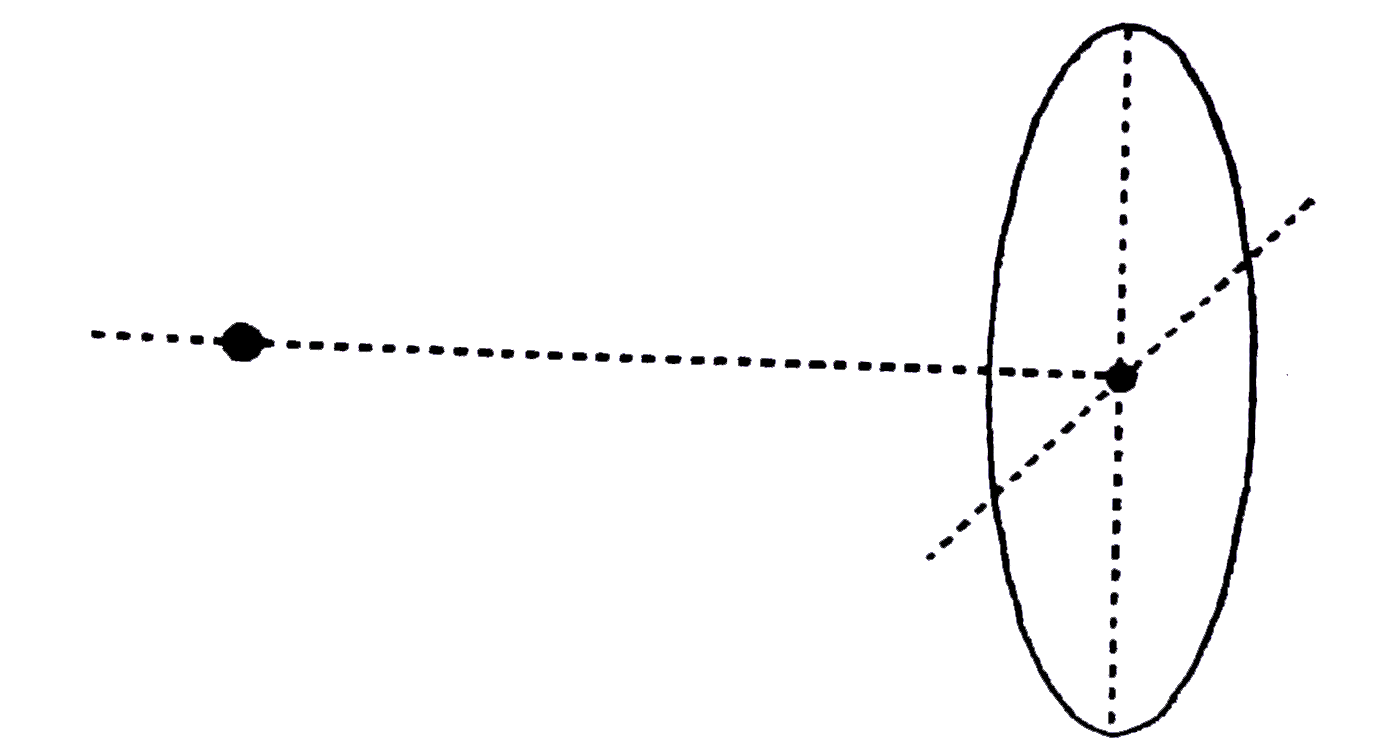
Column-IColumn-IIColumn-III(I)Maximum speed of the ring is v(i)Minimum speed of the particle isv/2(P)Final speed of the ring and particle is v and zero respectively.(II)Maximum speed of the ring isv/2(ii)Minimum speed of the particle is zero(Q)Final speed of the ring and particle is zero and v respectively.(III)Maximum speed of the ring isv2[1+√1−Qqπε0mrv2](iii)Minimum speed of the particle isv2[1+√1−Qqπε0mrv2](R)Final speed of the ring and particle is v/4 and3v/4 respectively.(IV)Maximum speed of the ring isv2[1−√1−Qqπε0mrv2](iv)Minimum speed of the particle isv2[1−√1−Qqπε0mrv2](S)Final speed of the ring and particle is v/2 for both.
Which of following options is the correct representation if v=√2Qqπε0mr
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring.

View SolutionCharge q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View SolutionCalculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring .The

View SolutionA charge q is uniformly distributed over a quarter circular ring of radius r. The magnitude of electric field strength at the centre of the ring will be
View SolutionA fixed ring of radius R is given a charge q. A charge q0 is brought slowly from infinity to the centre of the ring. The wrong statement is-
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionA current carrying ring is placed in a horizontal plane. A charged particle is dropped along the axis of the ring to fall under the influence of gravity
View Solution
