A fixed ring of radius R is given a charge q. A charge q0 is brought slowly from infinity to the centre of the ring. The wrong statement is-
work done by external agent in bringing q0 is 14πε0.qq0R when charge distribution is uniform
work done by external agent in bringing qc is 14πε0qq0R
force on q0 at the centre is zero, when charge distribution is uniform
force on q0 at the central is zero, when one half of the ring has positive charge and other half has negative charge
The correct Answer is:D
To solve the problem, we need to analyze the statements regarding the work done by an external agent when bringing a charge q0 to the center of a charged ring and the forces acting on q0 at that position.
1. Understanding the Setup:
- We have a fixed ring of radius R with a total charge q distributed uniformly along its circumference.
- A charge q0 is being brought from infinity to the center of the ring.
2. Statement 1 Analysis:
- The work done by an external agent in bringing q0 from infinity to the center of the ring can be calculated using the formula for electric potential energy.
- The electric field E at the center of the ring due to the charge q is zero because the contributions from all parts of the ring cancel out.
- Therefore, the work done W is given by:
W=∫0∞F⋅dr
- Since E=0 at the center, the force F on q0 is also zero, leading to:
W=0
- Thus, Statement 1 is true.
3. Statement 2 Analysis:
- This statement suggests that the work done is 14πϵ0⋅qq0R.
- This expression is incorrect because, as established earlier, the work done in bringing q0 to the center is zero.
- Hence, Statement 2 is false.
4. Statement 3 Analysis:
- This statement claims that the force on q0 at the center is zero when the charge distribution is uniform.
- As previously discussed, the electric field at the center of a uniformly charged ring is indeed zero, leading to zero force on q0.
- Therefore, Statement 3 is true.
5. Statement 4 Analysis:
- This statement claims that the force on q0 at the center is zero when one half of the ring has positive charge and the other half has negative charge.
- If one half of the ring has positive charge and the other half has negative charge, the forces exerted by the positive and negative charges on q0 will also cancel each other out.
- Thus, the force on q0 at the center will still be zero, making Statement 4 true.
Conclusion:
The wrong statement among the options provided is Statement 2.
- We have a fixed ring of radius R with a total charge q distributed uniformly along its circumference.
- A charge q0 is being brought from infinity to the center of the ring.
- The work done by an external agent in bringing q0 from infinity to the center of the ring can be calculated using the formula for electric potential energy.
- The electric field E at the center of the ring due to the charge q is zero because the contributions from all parts of the ring cancel out.
- Therefore, the work done W is given by:
W=∫0∞F⋅dr
- Since E=0 at the center, the force F on q0 is also zero, leading to:
W=0
- Thus, Statement 1 is true.
- This statement suggests that the work done is 14πϵ0⋅qq0R.
- This expression is incorrect because, as established earlier, the work done in bringing q0 to the center is zero.
- Hence, Statement 2 is false.
- This statement claims that the force on q0 at the center is zero when the charge distribution is uniform.
- As previously discussed, the electric field at the center of a uniformly charged ring is indeed zero, leading to zero force on q0.
- Therefore, Statement 3 is true.
- This statement claims that the force on q0 at the center is zero when one half of the ring has positive charge and the other half has negative charge.
- If one half of the ring has positive charge and the other half has negative charge, the forces exerted by the positive and negative charges on q0 will also cancel each other out.
- Thus, the force on q0 at the center will still be zero, making Statement 4 true.
The wrong statement among the options provided is Statement 2.
Topper's Solved these Questions
Similar Questions
A thin conducting ring of radius R is given a charge +Q, Fig. The electric field at the center O of the ring due to the charge on the part AKB of the ring is E. The electric field at the center due to the charge on part ACDB of the ring is

View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R/2 from the centre of the shell is
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionA thin circular wire of radius r has a charge Q. If a point charge q is placed at the centre of the ring, then find the increase in tension in the wire.
View SolutionA charge +Q is uniformly distributed over a thin ring with radius R. A negative point charge −Q and mass m starts from rest at a point far away from the centre of the ring and moves towards the centre. Find the velocity of this particle at the moment it passes through the centre of the ring .
View SolutionA ring of mass m1 and radius R is fixed in space at some location. An external agent brings a point mass m2 from infinity to centre of the ring. Work done by the external agent will be
View SolutionA half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
View SolutionEight charges each of value q are placed on a ring of radius R placed in x - y plane with origin at centre . A - q charge having mass m is projected from z=∞ towards the centre of the ring with velocity v . The velocity of - q when it reaches the centre of ring is (neglect gravity)
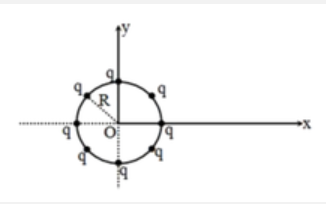
View SolutionA ring of radius R carries a uniformly distributed charge +Q. A point charge −q is placed on the axis of the ring at a distance 2R from the centre of the ring and released from rest. The particle executes a simple harmonic motion along the axis of the ring. State True or False.
View Solution