A graph between current and time during charging of a capacitor by a battery in series with a resistor is shown. The graphs are drawn for two circutis. R1,R2,C1,C2 and V1,V2 are the values of resistance, capacitance and EMF of the cell in the two circuits. If only two parameters (out of resistance, capacitance, EMF) are different in the two circuits. What may be the correct options (s) ?
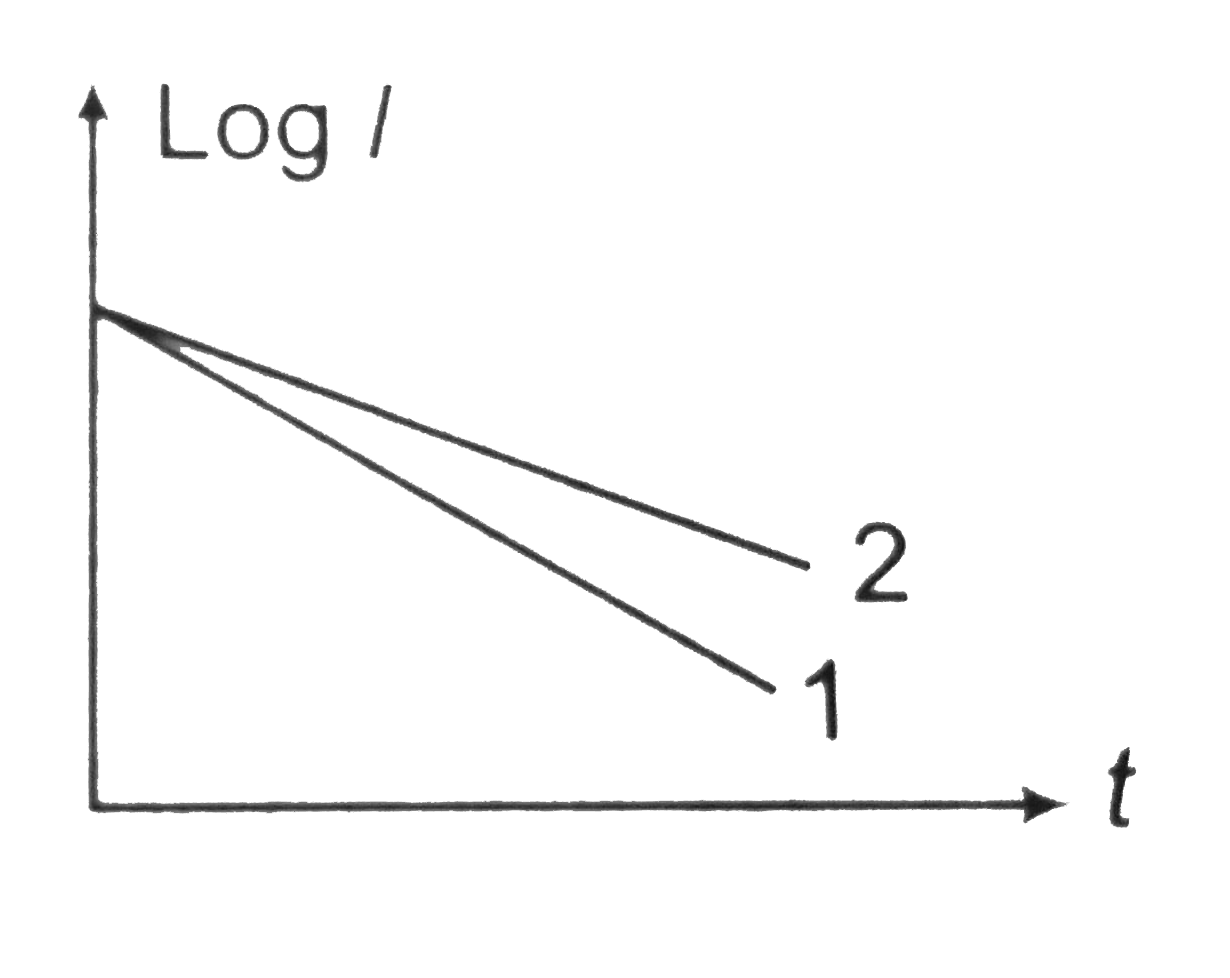
V1=V2,R1>R2,C1>C2
V1>V2,R1>R2,C1=C2
V1<V2,R1<R2,C1=C2
V1<V2,C1>C2,R1=R2
The correct Answer is:C
I=I0etRC
logI=logI0−tRC⇒logI=log(V0R)−tRC
from above equation only option (3) is correct.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A battery having 12V emf and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 1A, then the resistance of resistor and lost voltage of the battery when circuit is closed will be
A7Ω,7VB8Ω,8VC9Ω,9VD9Ω,10V
In the circuit shown, R1=2Ω,R2=R3=10ΩandE=6V. Work out the equivalent resistance of the circuit and the current in each resistor.
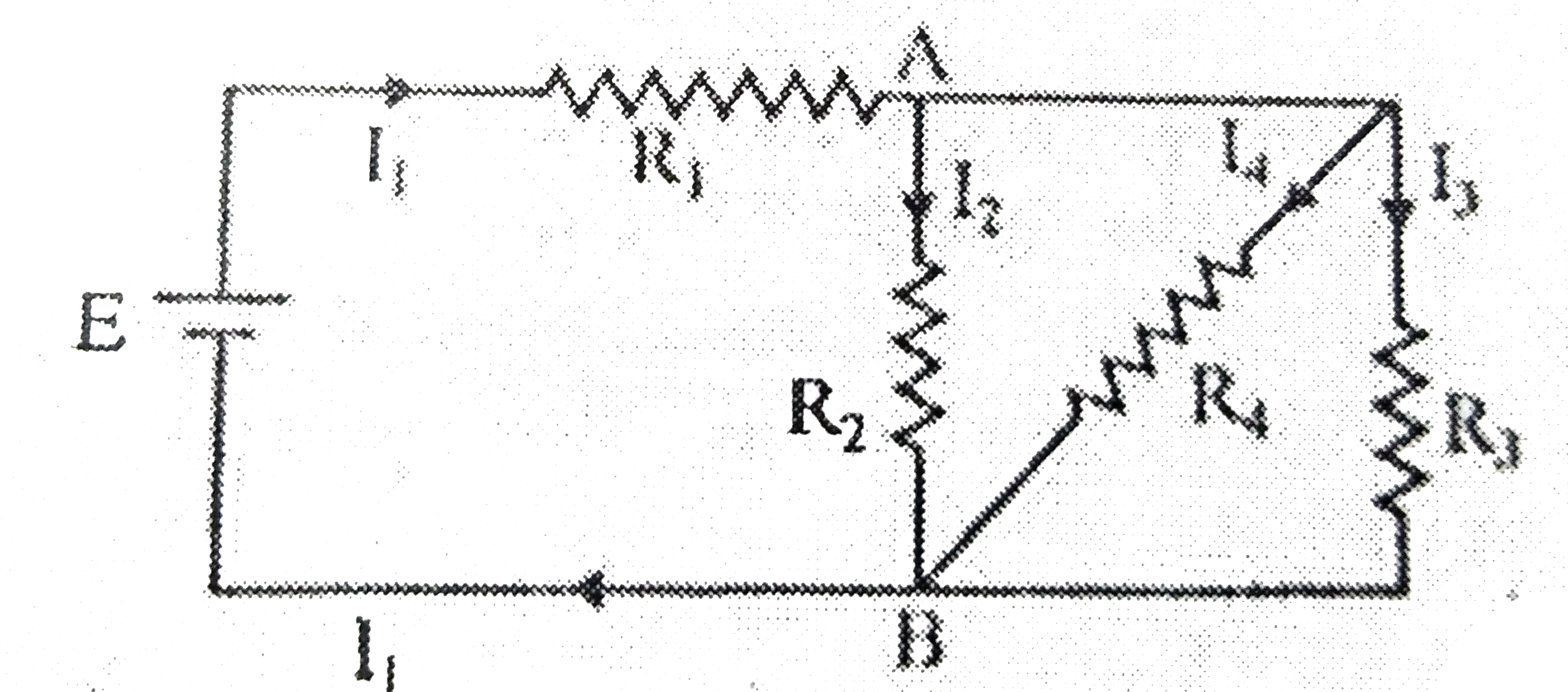
View SolutionIn a series combination of two capacitances C and C (Cgt C) (as shown in the circuit),
View SolutionIn the circuit shown, R1=2Ω,R2=R3=10Ω,R4=20ΩandE=6V. Work out the equivalent resistance of the circuit and the current in each resistor.
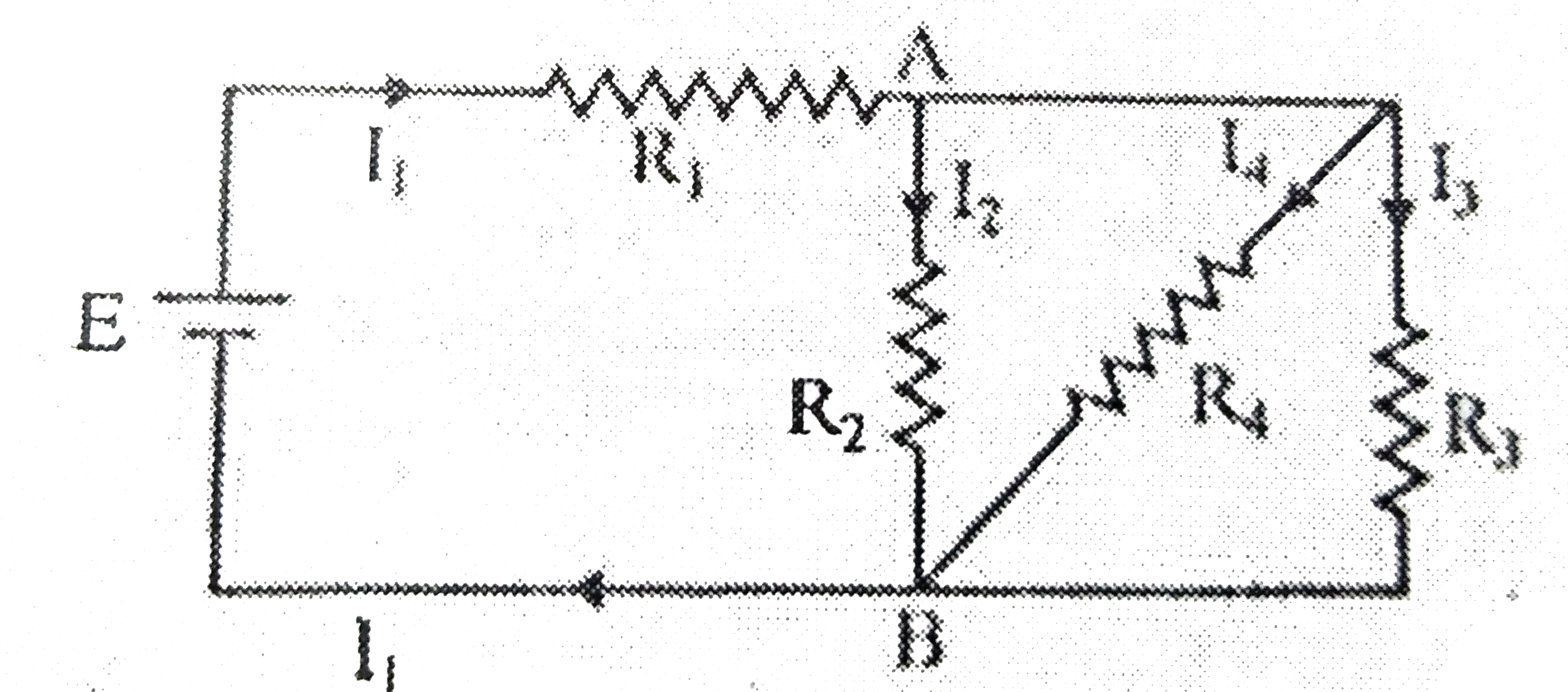
View SolutionA battery of emf 12V and internal resistance 2Ω is connected with two resistors A and B of resistance 4Ω and 6Ω respectively joined in series. . The current i in the circuit is
View SolutionA capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
View SolutionIn a series L-C-R circuit the voltage across resistance , capacitance and inductance is 10 V each. If the capacitance is short circuited, the voltage across the inductance will be
View SolutionEach of the resistors shown in figure has a resistances of 10(Ω)and each of the batteries has an emf of 10V.Find the currents through the resistors a and b in the two circuits.

View Solution

