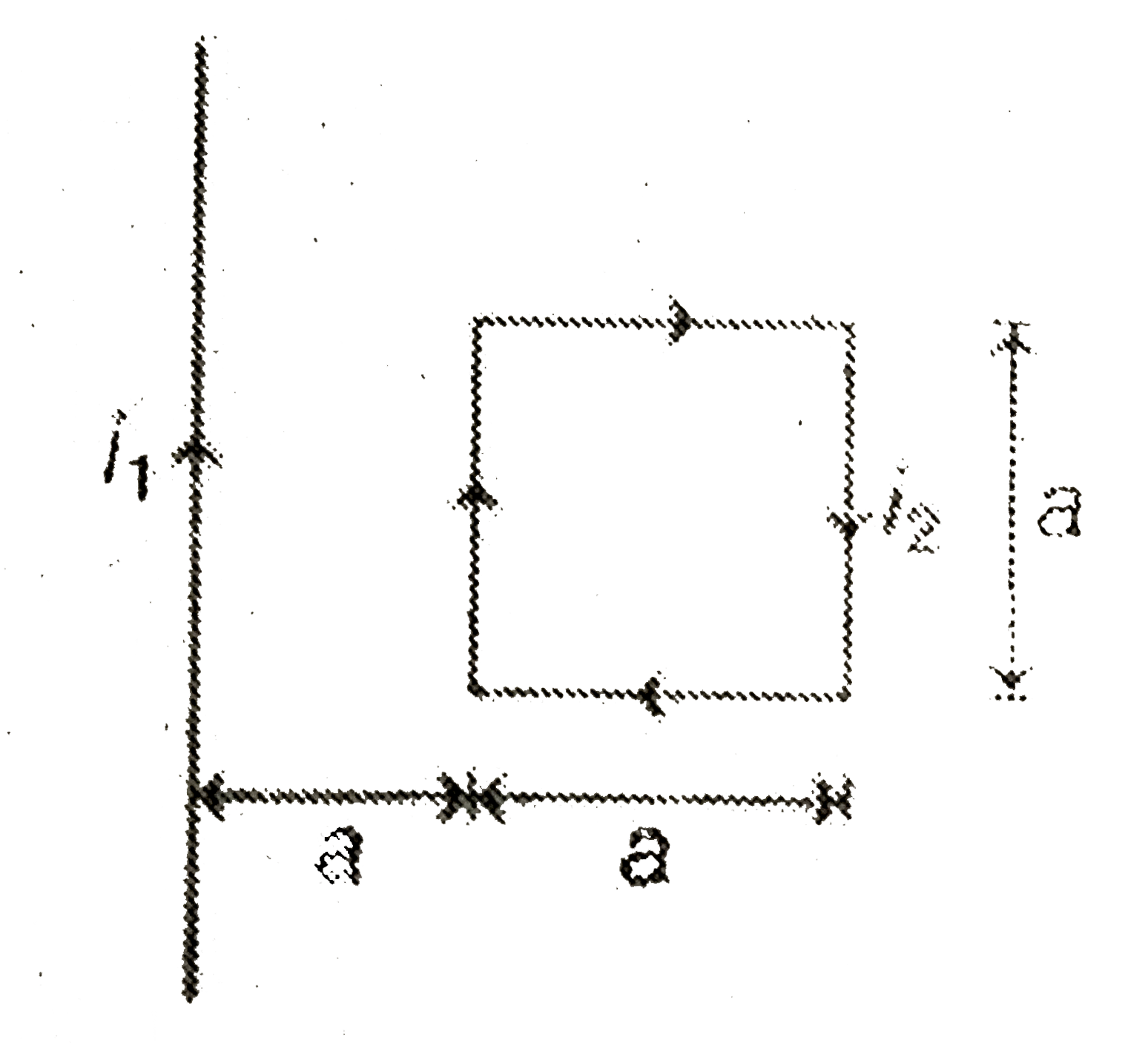
Three distinct current carrying wires intersect a finite rectangular plane ABCD. The current in left wire and the loop is . The direction of current in left most wire and right most loop is downwards as shown in figure. The current through middle wire is adjusted so that the path integral of the total magnetic field along the perimeter of the rectangle is zero, that is, . Then the current is-

A. and upwards
B. and downwards
C. and upwards
D. and downwards
and upwards
and downwards
and upwards
and downwards
The correct Answer is:C
For calculated of current upwards shall be positive and current downwards shall be negative Therefore,
Therefore upwards
Topper's Solved these Questions
Similar Questions
Three distinct current wires intersect a finite rectangular plane ABCD. The current is left wire and the loop is l1 . The direction of current in left most wire and righy most loop is downards as shown in the figure. The current l2through middle wire is adjusted so that the path integal of the total magnetic field along the perimeter of the rectangle is zero , that is ,∮ABCDA→B.d→s=0 then the current I2 is

View SolutionA current carrying wire is placed along east and west in a magnetic field directed north wards. If the current in the wire is directed east wards, the direction of force on the wire is
View SolutionA current carrying straight wire passing inside a triangular loop as shown in Figure. The current in the wire is perpendicular to paper inwards. Find the direction of the induced current in the loop if current in the wire is increased.

View SolutionA current carrying squre loop is placed near an infinitely long current carrying wire as shown in figure . The loop torque acting on the loop is
View SolutionShows a long current carrying wire and two rectangular loops moving with of velocity v. Find the direction of current in each loop.
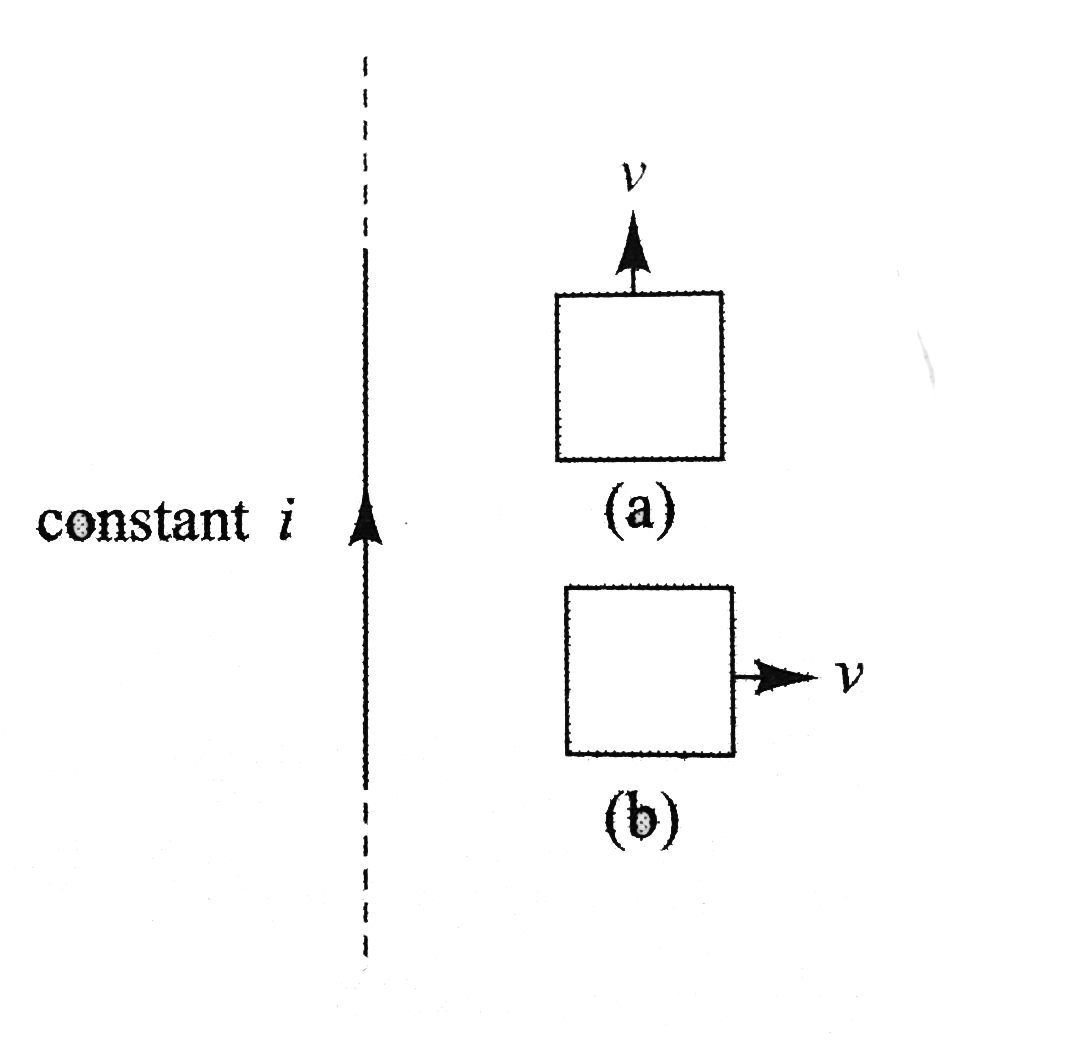
View SolutionShows a long current carrying wire and two rectangular loops moving with of velocity v. Find the direction of current in each loop.

View SolutionShows a long current carrying wire and two rectangular loops moving with of velocity v. Find the direction of current in each loop.

View SolutionA conductor loop is held above a current carrying wire 'PQ' as shown in figure. Depict the direction of the current induced in the loop when the current in the wire PQ is constanly increasing.

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

View Solution
