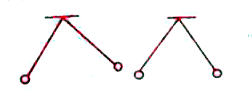
Two small spheres of masses M1 and M2 are suspended by weightless insulating threads of lengths L1 and L2. The spheres carry charges Q1 and Q2, respectively. The spheres are suspended such that they are in level with one another and the threads are inclined to the vertical at angle of θ1 and θ2 as shown. Which one of the following conditions is essential, if θ1=θ2?

m1=m2
|q1|=|q2|
l1=l2
q1m1=q2m2
The correct Answer is:A
Since both the small spheres are at same horizontal level, the electrostatic forces on both spheres are in horizontal direction. The FBD of left sphere is shown in figure.
∵ The sphere is equilibrium ⇒Tcosθ=mgandTsinθ=FE
∴tanθ=FEmg

The magnitude of electrostatic force on each sphere is same irrespective of its charge ∴ for θ1=θ2 the necessary condition is m1=m2
Topper's Solved these Questions
Similar Questions
Two small spheres of masses M1and M2 are suspended by weightless insulating threads of lengths L1 and L2. The spheres carry charges Q1 and Q2 respectively. The spheres are suspended such that they are in level with one another and the threads are inclined to the vertical at angles θ1 and θ2respectively . Which one of the following conditions is essential for θ1=θ2 ?
View SolutionCalculate θ1 and θ2 in shown situation.
_E01_244_Q01.png)
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionTwo positively charged sphere of masses m1 and m2 are suspended from a common point at the ceiling by identical insulating massless strings of length l. Charges on the two spheres are q1 and q2 respectively. Equilibrium both strings make the same angle θ with the vertical. then
View SolutionThe net field →E due to the uniformly charged rod at P makes angles θ1 and θ2 with AP and BP respectively. Then find the value of θ1/θ2

View SolutionThe locus of the point of intersection of two tangents to the parabola y2=4ax which make the angles θ1 and θ2 with the axis so that cot θ1+cotθ2 = k is
View SolutionThe locus of the point of intersection of two tangents to the parabola y2=4ax which make the angles θ1 and θ2 with the axis so that cot θ1+cotθ2 = c is
View SolutionTwo metal sphers of masses m1andm2 are suspended from a common point by a light insulting strings of same length. The length of each string is same. The spheres are given positive charges q1andq2. Figure A shows angles made by the strings with vertical are different where as for figure B same. Then, which of the following is possible
View Solutionθ1,θ2,θ3 are angles of 1st quadrant if tanθ1=cosθ1,tanθ2=cosecθ2,cosθ3=θ3. Which of the following is not true ?
View Solution