Two positively charged sphere of masses m1 and m2 are suspended from a common point at the ceiling by identical insulating massless strings of length l. Charges on the two spheres are q1 and q2 respectively. Equilibrium both strings make the same angle θ with the vertical. then
q1m2=q2m2
m1=m2
m1=m2sinθ
q2m1=q1m2
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on the two positively charged spheres suspended from a common point. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have two spheres of masses m1 and m2 that are positively charged with charges q1 and q2 respectively. They are suspended from the ceiling by identical massless strings of length l. Both strings make the same angle θ with the vertical.
Step 2: Analyze Forces on Each Sphere
For each sphere, there are three forces acting on it:
1. The gravitational force acting downward: Fg=mig (where i is either 1 or 2).
2. The tension T in the string acting along the string.
3. The electrostatic repulsive force F between the two charged spheres.
Step 3: Set Up the Equilibrium Conditions
In equilibrium, the net force acting on each sphere must be zero. This gives us two equations based on the forces acting on each sphere.
For sphere 1:
- The vertical component of the tension balances the weight:
Tcosθ=m1g
- The horizontal component of the tension balances the electrostatic force:
Tsinθ=F
For sphere 2:
- The vertical component of the tension balances the weight:
Tcosθ=m2g
- The horizontal component of the tension balances the electrostatic force:
Tsinθ=F′
Step 4: Relate the Forces
Since both spheres are at the same angle θ and are in equilibrium, we can equate the horizontal components of the forces:
Tsinθ=F(for sphere 1)
Tsinθ=F′(for sphere 2)
Step 5: Equate the Tension Forces
From the vertical force balance equations, we have:
T=m1gcosθ(for sphere 1)
T=m2gcosθ(for sphere 2)
Setting these equal gives:
m1gcosθ=m2gcosθ
Since g and cosθ are common, we can simplify this to:
m1=m2
Conclusion
Thus, we conclude that the masses of the two spheres are equal:
m1=m2
We have two spheres of masses m1 and m2 that are positively charged with charges q1 and q2 respectively. They are suspended from the ceiling by identical massless strings of length l. Both strings make the same angle θ with the vertical.
For each sphere, there are three forces acting on it:
1. The gravitational force acting downward: Fg=mig (where i is either 1 or 2).
2. The tension T in the string acting along the string.
3. The electrostatic repulsive force F between the two charged spheres.
In equilibrium, the net force acting on each sphere must be zero. This gives us two equations based on the forces acting on each sphere.
- The vertical component of the tension balances the weight:
Tcosθ=m1g
- The horizontal component of the tension balances the electrostatic force:
Tsinθ=F
- The vertical component of the tension balances the weight:
Tcosθ=m2g
- The horizontal component of the tension balances the electrostatic force:
Tsinθ=F′
Since both spheres are at the same angle θ and are in equilibrium, we can equate the horizontal components of the forces:
Tsinθ=F(for sphere 1)
Tsinθ=F′(for sphere 2)
From the vertical force balance equations, we have:
T=m1gcosθ(for sphere 1)
T=m2gcosθ(for sphere 2)
m1gcosθ=m2gcosθ
Since g and cosθ are common, we can simplify this to:
m1=m2
Thus, we conclude that the masses of the two spheres are equal:
m1=m2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.44
Explore 10 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.45
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.42
Explore 20 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
Two metal sphers of masses m1andm2 are suspended from a common point by a light insulting strings of same length. The length of each string is same. The spheres are given positive charges q1andq2. Figure A shows angles made by the strings with vertical are different where as for figure B same. Then, which of the following is possible
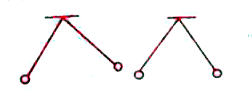
View SolutionTwo small spheres of masses M1and M2 are suspended by weightless insulating threads of lengths L1 and L2. The spheres carry charges Q1 and Q2 respectively. The spheres are suspended such that they are in level with one another and the threads are inclined to the vertical at angles θ1 and θ2respectively . Which one of the following conditions is essential for θ1=θ2 ?
View SolutionThree paricles, each of mass m and carrying a charge q each, are suspended from a common pointby insulating massless strings each of length L. If the particles are in equilibrium and are located at the corners of an equilateral triangle of side a, calculate the charge q on each particle. Assume L>>a.
View SolutionTwo small spheres, each having a mass of 20 g, are suspended form a common point by two insulating strings of length 40 cm each. The spheres are identically charged and the speration between the balls at equilibrium is found to be 4 cm . Find the charge on each sphere.
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View SolutionTwo identical pendulums A and B are suspended from the same point. Both are given positive charge, with A having more charge than B. They diverge and reach equilibrium with the suspension of A and B making angles θ1andθ2 with the vertical respectively.
View SolutionTwo identical charged spheres of material density ρ, suspended from the same point by inextensible strings of equal length make an angle θ between the string. When suspended in a liquid of density σ the angle θ remains the same. The dielectric constant K of the liquid is
View SolutionTwo identical charged spheres suspended from a common point by two mass-less strings of length l are initially at a distance d ( d<<l) apart because of their mutual repulsion . The charge begins to leak from both the spheres at a constant rate. As a result the charge approach each other with a velocity v. Then as a function of distance x between them .
View SolutionThe positions of two point charges q1 and q2 are →r1 and →r2 , respectively. Find the position of the point where the net field is zero due to thses charges.
View Solution