A body moves in a circular orbit of radius R under the action of a central force. Potential due to the central force is given by V(r) = kr (k is a positive constant). Period of revolution of the body is proportional to-
R1/2
R−1/2
R−3/2
R−5/2
The correct Answer is:A
To solve the problem, we need to determine how the period of revolution T of a body moving in a circular orbit under a central force relates to the radius R of the orbit, given that the potential V(r)=kr, where k is a positive constant.
1. Identify the Potential Energy:
The potential energy due to the central force is given by:
V(r)=kr
2. Calculate the Central Force:
The force F associated with this potential is obtained by taking the negative gradient of the potential energy:
F=−dVdr=−d(kr)dr=−k
Since we are dealing with a central force, we consider the magnitude:
F=k
3. Equate to Centripetal Force:
For a body moving in a circular path of radius R with mass m and speed v, the centripetal force required is given by:
Fc=mv2R
Setting the central force equal to the centripetal force gives:
k=mv2R
4. Solve for Velocity:
Rearranging the equation to solve for v2:
mv2=kR⟹v2=kRm
Taking the square root gives:
v=√kRm
5. Determine the Period of Revolution:
The period T of revolution is given by the formula:
T=2πRv
Substituting the expression for v:
T=2πR√kRm
Simplifying this expression:
T=2πR⋅√mkR=2π√mk⋅√R
6. Final Expression:
Therefore, we find that the period T is proportional to R1/2:
T∝R1/2
Conclusion:
The period of revolution T of the body is proportional to the square root of the radius R of its circular orbit.
The potential energy due to the central force is given by:
V(r)=kr
The force F associated with this potential is obtained by taking the negative gradient of the potential energy:
F=−dVdr=−d(kr)dr=−k
Since we are dealing with a central force, we consider the magnitude:
F=k
For a body moving in a circular path of radius R with mass m and speed v, the centripetal force required is given by:
Fc=mv2R
Setting the central force equal to the centripetal force gives:
k=mv2R
Rearranging the equation to solve for v2:
mv2=kR⟹v2=kRm
Taking the square root gives:
v=√kRm
The period T of revolution is given by the formula:
T=2πRv
Substituting the expression for v:
T=2πR√kRm
Simplifying this expression:
T=2πR⋅√mkR=2π√mk⋅√R
Therefore, we find that the period T is proportional to R1/2:
T∝R1/2
The period of revolution T of the body is proportional to the square root of the radius R of its circular orbit.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.44
10 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.45
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.42
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
An electron moves in circular orbit of radius r with constant speed v.The force acting in it is
View SolutionA particle is moving in a circular path of radius a under the action of an attractive potential U=−k2r2. Its total energy is :
View SolutionA body is moving with an acceleration 'a' under the action of a force 'g'. The weight of the body is
View SolutionAn electron of mass m, moves around the nucleus in a circular orbit of radius .r. under the action of centripetal force .F.. The equivalent electric current is
View SolutionA particle of mass M moves with constant speed along a circular path of radius r under the action of a force F. Its speed is
View SolutionA particle is moving in a circular path of radius r under the action of a force F. If at an instant velocity of particle is v, and speed of particle is increasing, then
View SolutionA small planet is revolving around a massive star in a circular orbit of radius R with a period of revolution T. If the gravitational force between the planet and the star were proportional to R−5/2, then T would be proportional to
View SolutionAn object of mass m moves with constant speed in a circular path of radius r under the action of a force of constant magnitude F. the kinetic energy of object is
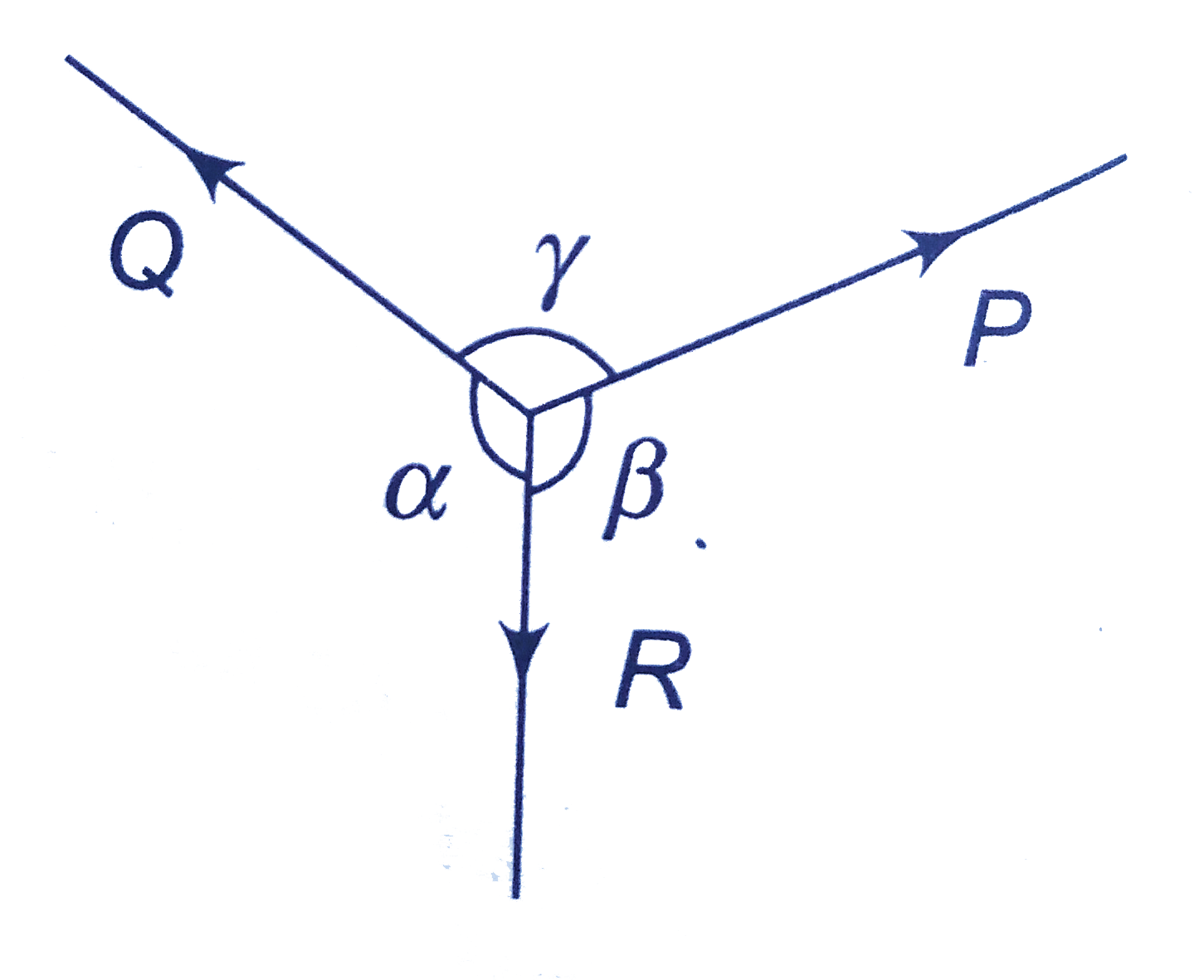
View SolutionA body is in equilibrium under the action of three coplanar forces P,QandR as shown in figure. Select the correct statement.
View SolutionA particle is moving with a uniform speed in a circular orbit of radius R in a central force inversely proportional to the nth power of R. If the period of rotation of the particle is T, then :
View Solution
