A double slit is illuminated by light of wavelength 12000 A .the slits are 0.1 cm apart and the screen is placed one metre away .find the sepration between the two adjacent minima?
The correct Answer is:4
To solve the problem of finding the separation between two adjacent minima in a double slit experiment, we can follow these steps:
Step 1: Understand the given parameters
- Wavelength of light (λ) = 12000 Å (Angstroms)
- Distance between the slits (d) = 0.1 cm
- Distance from the slits to the screen (D) = 1 m
Step 2: Convert the units
- Convert the wavelength from Angstroms to meters:
1 Å=10−10 m
Therefore,
λ=12000 Å=12000×10−10 m=1.2×10−6 m
- Convert the distance between the slits from cm to meters:
d=0.1 cm=0.1×10−2 m=1×10−3 m
Step 3: Use the formula for fringe width (β)
The formula for fringe width (β) in a double slit experiment is given by:
β=λDd
Where:
- λ = wavelength of light
- D = distance from the slits to the screen
- d = distance between the slits
Step 4: Substitute the values into the formula
Substituting the values we have:
β=(1.2×10−6 m)(1 m)1×10−3 m
Step 5: Calculate the fringe width
Calculating the above expression:
β=1.2×10−61×10−3=1.2×10−3 m
This can also be expressed in millimeters:
β=1.2 mm
Step 6: Find the separation between two adjacent minima
The separation between two adjacent minima is equal to the fringe width (β). Thus, the separation between the two adjacent minima is:
Separation=1.2 mm
Final Answer
The separation between the two adjacent minima is 1.2 mm.
---
- Wavelength of light (λ) = 12000 Å (Angstroms)
- Distance between the slits (d) = 0.1 cm
- Distance from the slits to the screen (D) = 1 m
- Convert the wavelength from Angstroms to meters:
1 Å=10−10 m
Therefore,
λ=12000 Å=12000×10−10 m=1.2×10−6 m
d=0.1 cm=0.1×10−2 m=1×10−3 m
The formula for fringe width (β) in a double slit experiment is given by:
β=λDd
Where:
- λ = wavelength of light
- D = distance from the slits to the screen
- d = distance between the slits
Substituting the values we have:
β=(1.2×10−6 m)(1 m)1×10−3 m
Calculating the above expression:
β=1.2×10−61×10−3=1.2×10−3 m
This can also be expressed in millimeters:
β=1.2 mm
The separation between two adjacent minima is equal to the fringe width (β). Thus, the separation between the two adjacent minima is:
Separation=1.2 mm
The separation between the two adjacent minima is 1.2 mm.
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physic
48 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS
17 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - Part-1 Physics
15 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
A double slit is illuminated by light of wavelength 6000 Å. The slits are 0.1 cm apart and the screen is placed one metre away. calculate :
sepration between the two adjacent minima
View SolutionA double slit is illuminated by the light of wavelength 12000A .The slits are 0.1 cm apart and the screen is placed one metre away.calculate the sepration between the two adjacent minima?
View Solution
Knowledge Check
A single slit is illuminated by light of wavelength 6000 Ã…. The slit width is 0.1 cm and the screen is placed 1 m away. The angular position of 10th minimum in radian is
A2×10−4B6×10−3C3×10−3D1×10−4In double slit experiment using light of wavelength 600nm, the angular width of a fringe formed on a distant screen is 0.1∘. What is the spacing between the two slits ?
A3.44×10−4mB1.54×10−4mC1.54×10−3mD1.44×10−3m
A double slit is illuminated by the light of wavelength 12000A .The slits are 0.1 cm apart and the screen is placed one metre away.calculate the angular posiyion of 10 maximum in radians ?
View SolutionA double slit is illuminated by light of wave length 6000 Å. The slit are 0.1 cm apart and the screen is placed one metre away. Calculate.
(i). The angular position of the 10th maximum in radian and
(ii). Separation of the two adjacent minimal.
View SolutionTwo slits, 4 mm apart, are illuminated by light of wavelength 6000Å. What will be the fringe width on a screen placed 2 m from the slits
View SolutionIn Young.s double slit experiment, blue-green light of wavelength 500nm is used. The slits are 1.20mm apart, and the viewing screen is 5.40m away from the slits. What is the fringe width.
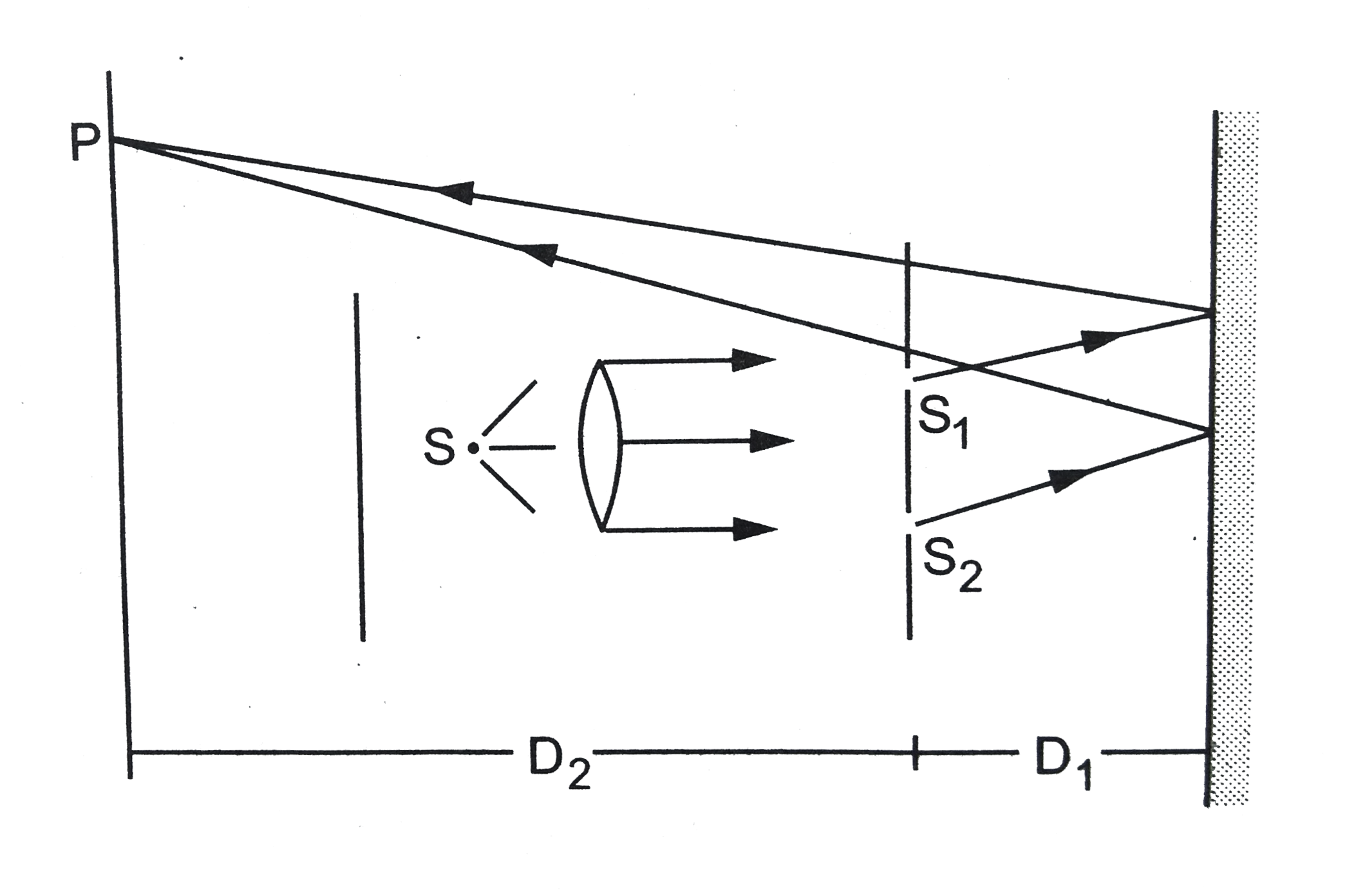
View SolutionA double slit S1−S2 is illuminated by a coherent light of wavelength λ. The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1, from it and a screen ∑ is placed behind the double slit at a distance D2, from it . The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
View SolutionIn double slit experiment using light of wavelength 600nm, the angular width of a fringe formed on a distant screen is 0.1∘. What is the spacing between the two slits ?
View Solution
