A trinary star system which is a system of three orbiting around centre of mass of system has time peroid of 3 years, while the distance between any two stars of the system is 2 astronomical unit. All the three stars are identical and mass of the sun is M and total mass of this multiple star system is ab×M . Then find b3? (a and b are lowest possible integers (I astronomical unit is equal to distance between sun and earth, time period of rotation of earth around sun is 1year)
The correct Answer is:3
To solve the problem, we need to analyze the trinary star system and apply the principles of gravitational force and centripetal motion. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the System
We have a trinary star system with three identical stars, each having mass m0. The distance between any two stars is given as 2 astronomical units (AU). The time period of the system's rotation around the center of mass is T=3 years.
Step 2: Determine the Geometry
The stars form an equilateral triangle due to their identical masses. The distance between any two stars is 2 AU. The radius r from the center of mass to each star can be derived using geometry.
In an equilateral triangle, if the side length is s, the distance from the center to a vertex (the radius) is given by:
r=s√3
For our case, s=2 AU, so:
r=2 AU√3=2√3 AU
Step 3: Apply Gravitational Force
The gravitational force between two stars can be expressed as:
F=Gm20(2 AU)2
However, since we have three stars, we need to consider the net gravitational force acting on one star due to the other two.
Step 4: Calculate the Net Force
The net force acting on one star due to the other two can be calculated by considering the components of the forces. The angle between the forces from the two other stars is 60∘. The resultant force directed towards the center can be calculated as:
Fnet=2Fcos(30∘)=2(Gm20(2 AU)2)(√32)=Gm20√32 AU2
Step 5: Relate to Centripetal Force
This net gravitational force provides the necessary centripetal force for circular motion:
Fcentripetal=m0v2r
where v is the orbital speed of the stars. The angular velocity ω can be expressed in terms of the time period T:
ω=2πT=2π3 years
The relationship between linear velocity and angular velocity is:
v=rω
Step 6: Substitute and Solve
Substituting v into the centripetal force equation:
Fcentripetal=m0(rω)2r=m0rω2
Setting the gravitational force equal to the centripetal force gives:
Gm20√32 AU2=m0r(2π3)2
Substituting r=2√3 AU:
Gm20√32 AU2=m0(2√3)(2π3)2
Step 7: Solve for m0
After simplifying, we can solve for m0 in terms of M (mass of the Sun):
m0=827M
Step 8: Total Mass of the System
The total mass of the system Mtotal is:
Mtotal=3m0=3(827M)=2427M=89M
Step 9: Find b3
From the total mass expression abM, we have a=8 and b=9. Thus:
b3=93=3
Final Answer
The value of b3 is 3.
We have a trinary star system with three identical stars, each having mass m0. The distance between any two stars is given as 2 astronomical units (AU). The time period of the system's rotation around the center of mass is T=3 years.
The stars form an equilateral triangle due to their identical masses. The distance between any two stars is 2 AU. The radius r from the center of mass to each star can be derived using geometry.
r=s√3
For our case, s=2 AU, so:
r=2 AU√3=2√3 AU
The gravitational force between two stars can be expressed as:
F=Gm20(2 AU)2
However, since we have three stars, we need to consider the net gravitational force acting on one star due to the other two.
The net force acting on one star due to the other two can be calculated by considering the components of the forces. The angle between the forces from the two other stars is 60∘. The resultant force directed towards the center can be calculated as:
Fnet=2Fcos(30∘)=2(Gm20(2 AU)2)(√32)=Gm20√32 AU2
This net gravitational force provides the necessary centripetal force for circular motion:
Fcentripetal=m0v2r
where v is the orbital speed of the stars. The angular velocity ω can be expressed in terms of the time period T:
ω=2πT=2π3 years
The relationship between linear velocity and angular velocity is:
v=rω
Substituting v into the centripetal force equation:
Fcentripetal=m0(rω)2r=m0rω2
Setting the gravitational force equal to the centripetal force gives:
Gm20√32 AU2=m0r(2π3)2
Substituting r=2√3 AU:
Gm20√32 AU2=m0(2√3)(2π3)2
After simplifying, we can solve for m0 in terms of M (mass of the Sun):
m0=827M
The total mass of the system Mtotal is:
Mtotal=3m0=3(827M)=2427M=89M
From the total mass expression abM, we have a=8 and b=9. Thus:
b3=93=3
The value of b3 is 3.
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physic
48 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PHYSICS
17 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - Part-1 Physics
15 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
Knowledge Check
The velocity of centre of mass of the system remains constant, if the total external force acting on the system is.
Aa. minimumBb. maximumCc. unityDd. zero
The center of mass of a system of two particles divides the distance between them.
View SolutionThe magnitude of acceleration of centre of mass of the system is

View SolutionThe momentum of a system with respect to centre of mass
View SolutionThe position of centre of mass of system of particles at any moment does not depend on.
View SolutionA binary star has a time period 3 years (time period of earth is one year) while distance between the two stars is 9 times distance between earth and the sun. Mass of one star is equal to mass of the sun and mass of other is 20n times mass of the sun then calculate n.
View SolutionIf three rods of same mass are placed as shown in the figure, the co-ordinates of the centre of mass of the system are
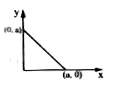
View SolutionTwo point masses m and 3m are placed at distance r. The moment of inertia of the system about an axis passing through the centre of mass of system and perpendicular to the joining the point masses is
View Solution