Find the center of mass (x,y,z) of the following structure of four idential cubes if the length of each side of a cube is 1 unit.
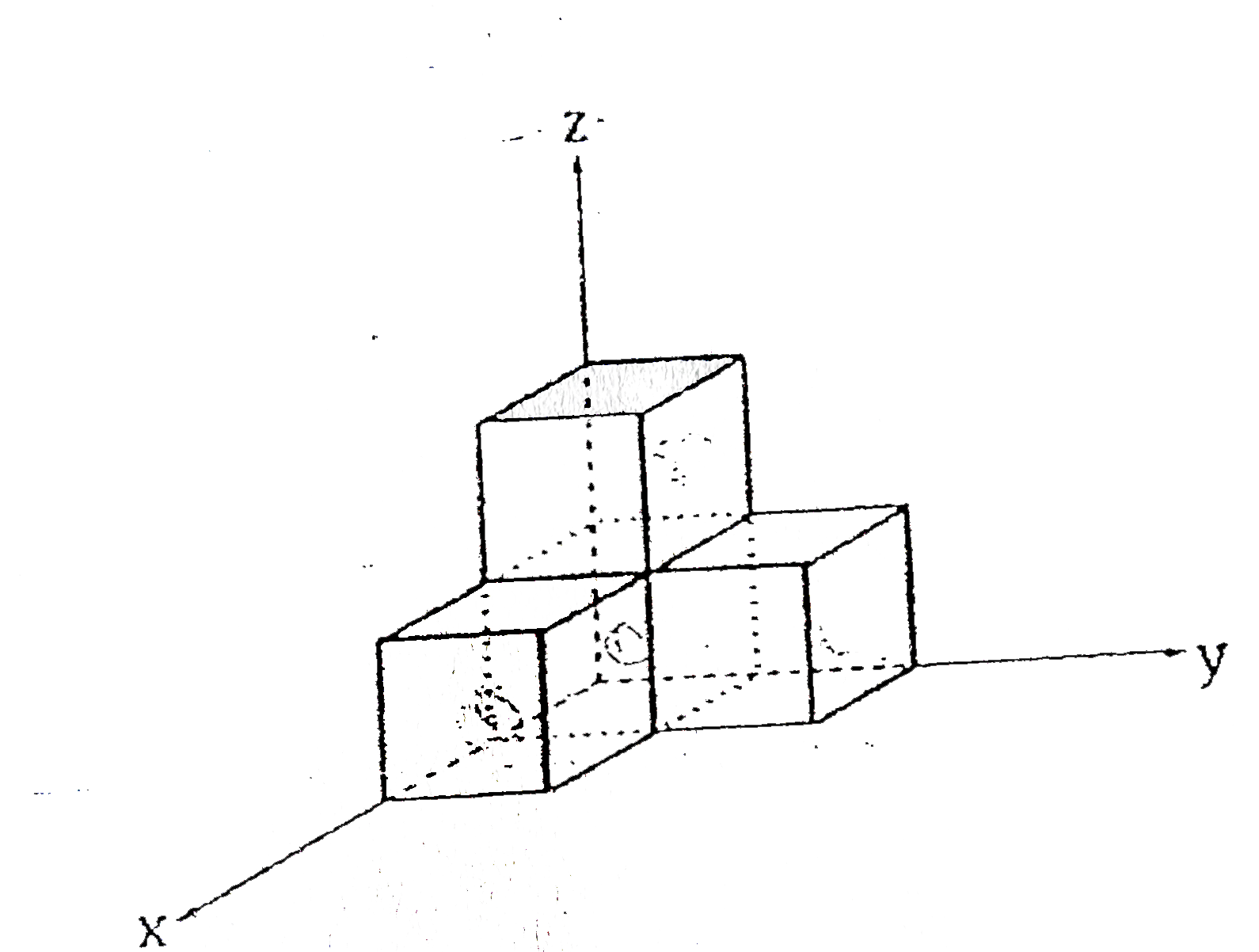
(1/2,1/2,1/2
(1/3,1/3,1/3)
(3/4,3/4,3/4)
(1/2,3/4,1/2)
The correct Answer is:(C )
First we find the centre of mass of each cube. It is located by symmetry: (0.5,0.5,0.5),(1.5,0.5,0.5),(0.5,1.5,0.5),(0.5,0.5,1.5). Now we find the centre of mass by treating the COM of each cube as a point particle:
xCOM=0.5+1.5+0.5+0.54=0.75,yCOM=0.5+0.5+1.5+0.54=0.75
zCOM=0.5+0.5+0.5+1.54=0.75
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Find the center of mass(x,y,z) of the following structure of four identical cubes if the length of each side of a cube is 1 unit.

View SolutionFind the cube of : x−12
View SolutionAt each point on the surface of the cube shown in the figure, the electric field is parllel to the z- axis. The length of each edge of the cube is 3.0 m on the bottom face it is →E=34ˆkN/C and on the bottom face it is →E=20ˆkN/C . Find the net flux contained within the cube.
View SolutionFind x,y and z in each of the following figure:

View SolutionFour identical cubes are joined end to end to form a cuboid .If the total surface area of the resulting cuboid is 648 cm2 .Find the length of edge of each cube.
View SolutionFour identical cubes are joined end to end to form a cuboid. If the total surface area of the resulting cuboid is 648 cm2, find the length of edge of each cube.
Also, find the ratio between the surface area of the resulting cuboid and the surface area of a cube.
View SolutionFour identical cubes are joined end to end to form a cuboid. If the total surface area of the resulting cuboid is 684cm2, find the length of edge of each cube. Also, find the ratio between the surface area of the resulting cuboid and the surface area of a cube.
View SolutionFind the cube of : (v) 2x+1x
View SolutionA uniform cube of mass M is floating on the surface of a liquid with three fourth of its volume immersed in the liquid (density=ρ). The length of the side of the cube is equal to

View SolutionA cube is arranged such that its length, breadth and height are along X, Y and Z directions, One of its corners is situated a the origin. Length of each side of the cube is 25cm. The components of electric field are Ex=400√2N/C,Ey=0andEz=0 respectively. Find the flux coming out of the cube at one end.
View Solution
