A car P is moving with a uniform speed 5√3m/s towards a carriage of mass 9 kg at rest kept on the rails at a point B as shown in the figure. The height AC is 120 m. Cannon balls of 1 kg are fired from the car with an initial velocity 100 m/s with respect to the car at an angle 30∘ with the horizontal.

The first cannon ball hits the stationary carriage after a time t0 and sticks to it. Determine t0. (in sec)
The correct Answer is:12s,15.75ms−1
Consider the vertical motion of th ecannon ball
∴S=ut+12at2∴−120=50t0−5t20
⇒5t20−5t0−120=0⇒t20−10t0−24=0
∴t0=−(−10)±[√100−4(1)(−24))2=12 or −2
The horizontal velocity of the cannon ball remains the same
∴vx=100cos30∘+5√3=55√3m/s
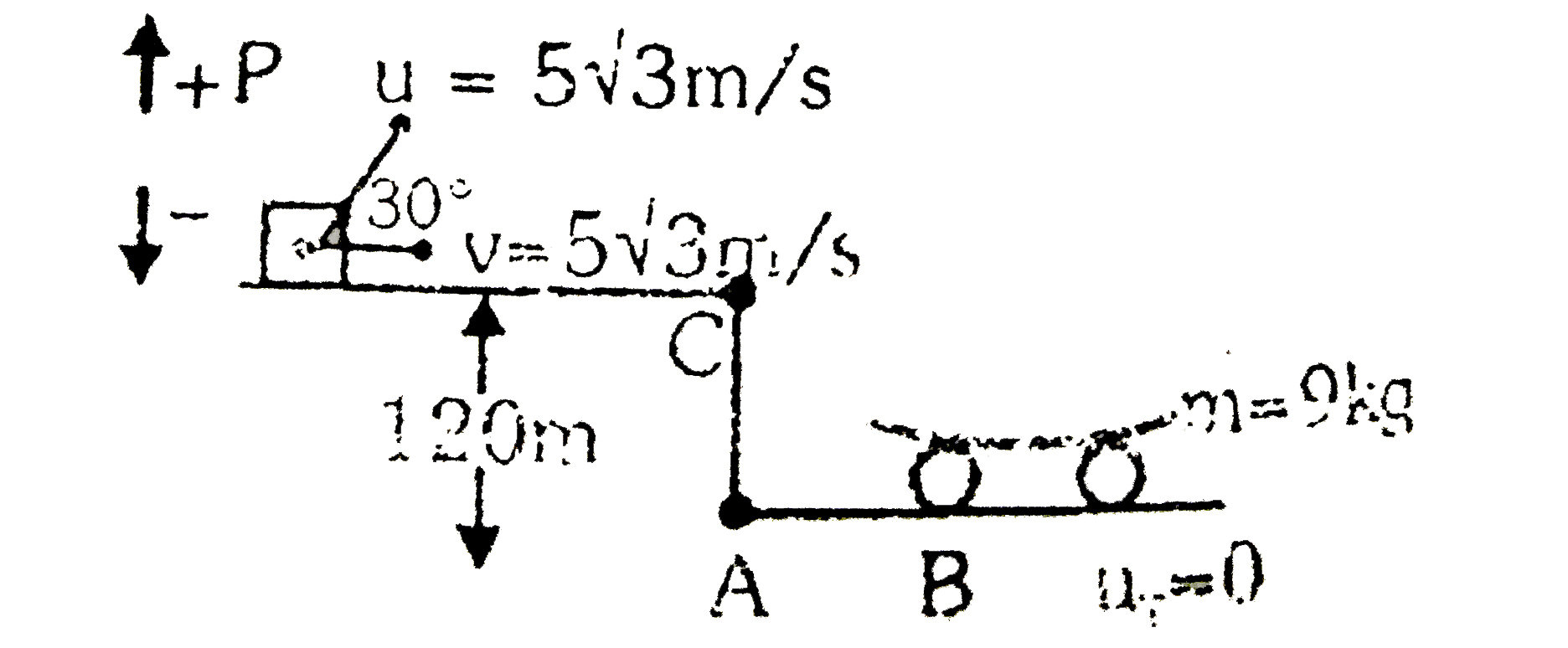
∴ Apply conservation of linear momentum to the cannon ball-trolley system in horizontal direction. If m is the mass of cannon ball and M is the mass of the trolley then
mvx+M×0=(m+M)Vx∴Vx=mvxm+M
where vx is the velocity of the (cannon ball - trollwy) system
Vx=1×55√31+9=5.5√3m/s
The second ball was projected after 12 second
Horizontal distance covered by the car
P=12×5√3=60√3m
Since the second ball also struck the trollwy
⇒ In time 12 seconds the trolley covers a distance of 60√3
For trolley in 12sec
From s=(u+v2)60√3=(5.5√3+v2)(12)⇒v=7.8m/s
To find the final velocity of the carriage after the second impact we again apply conservation of linear momentum in th ehorizontal direction
mvx+(M+m)7.8=(M+2m)vf
∴1×55√3+(9+1)7.8=(9+2)vf
⇒vf=15.75m/s
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A
20 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A flat car of mass M is at rest on a frictionless floor with a child of mass m standing at its edge. If the child jumps off from the car towards right with an initial velocity u, with respect to the car, find the velocity of the car after its jump.
View SolutionA cannon of mass 100 kg is kept on a frictionless floor. If a cannon ball of mass 1 kg is fired from it with a speed of 200 m/s. With what velocity the cannon will move ?
View SolutionA rail road car of mass M is at rest on frictionless rails when a man of mass m starts moving on the car towards the engine. If the car recoils with a speed v backward on the rails, with what velocity is the man aproaching the engine?
View SolutionA car is travelling at a velocity of 10 m/s and has a mass of 850 kg. What is its kinetic energy?
View SolutionOut of the two cars A and B car A is moving towards east with velocity of 10 m/s whereas B is moving towards north with a velocity 20 m/s, then velocity of A w.r.t B is ( nearly )
View SolutionA ball of mass 1kg is thrown up with an initial speed of 4m/s. A second ball of mass 2kg is released from rest from some height as shown in Fig. Choose the correct statement (s).
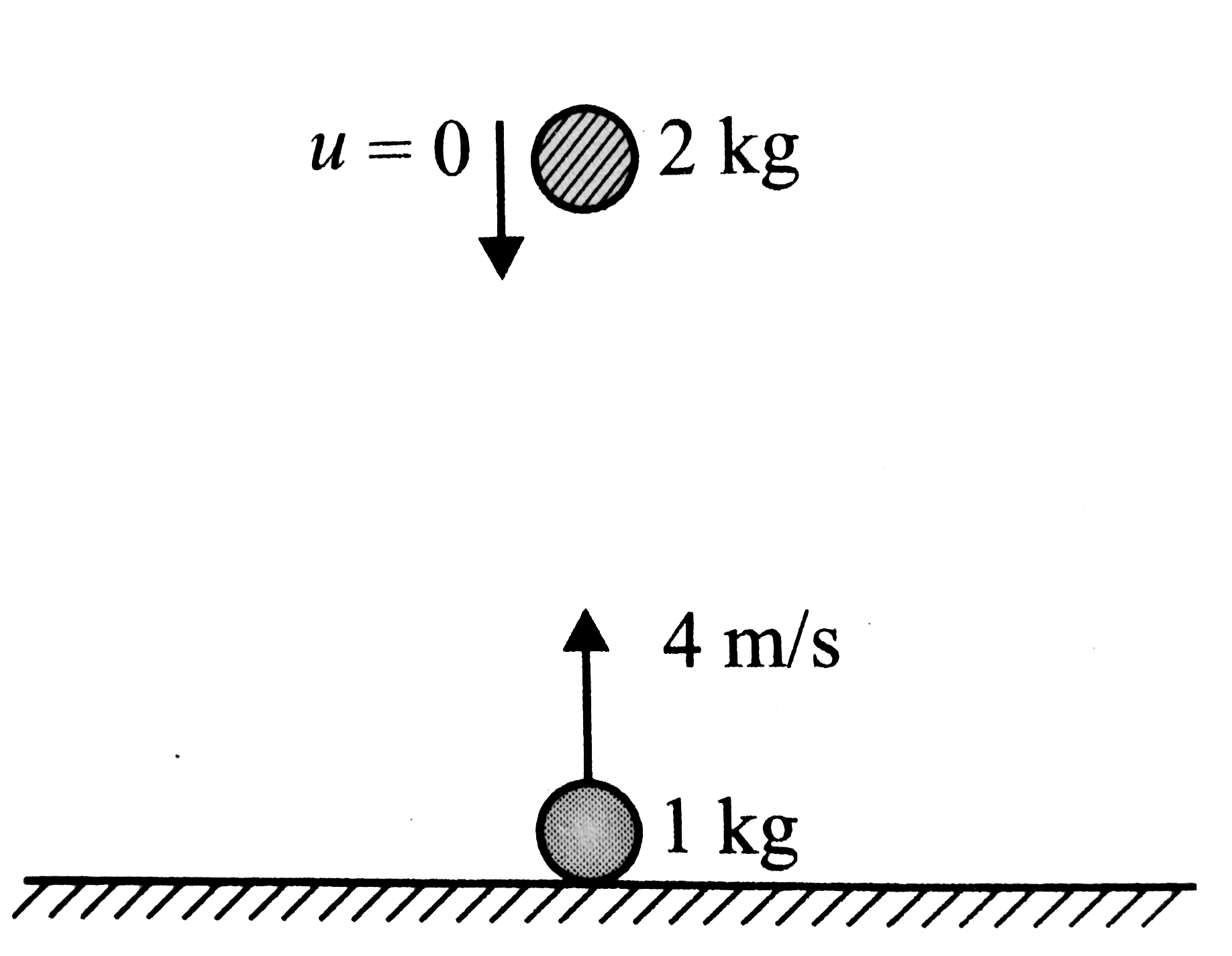
View SolutionA car is moving at a speed of 40 m/s on a circular track of radius 400 m. this speed is increasing at the rate of 3 m/s2. The acceleration of car is
View SolutionTwo cars A and B start moving from the same point with same velocity v=5km/minute. Car A moves towards North and car B in moving towards East. What is the relative velocity of B with respect to A ?
View SolutionA car is moving with constant speed of 10m/s on a horizontal circular path of radius 10√3m . A bob of mass m suspended through a light string from the roof of the car. What is the angle made by the string with the vertical if the bob is stationary with respect to the car? (g = 10 m/s2)
View SolutionA car of mass M is moving with a uniform velocity υ on a horizontal road when the hero of a Hindi film drops himself on it from above. Taking the mass of the hero to be m what will be the velocity of the car after the event?
View Solution
