A cannon of mass 100 kg is kept on a frictionless floor. If a cannon ball of mass 1 kg is fired from it with a speed of 200 m/s. With what velocity the cannon will move ?
To solve the problem, we will use the principle of conservation of momentum. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the system
We have a cannon of mass mc=100kg and a cannonball of mass mb=1kg. The cannonball is fired with a velocity vb=200m/s. The cannon is initially at rest.
Step 2: Write the conservation of momentum equation
According to the law of conservation of momentum, the total momentum before firing the cannonball must equal the total momentum after firing.
Initial momentum=Final momentum
Step 3: Calculate initial momentum
Since both the cannon and the cannonball are initially at rest, the initial momentum is:
Initial momentum=0
Step 4: Write the final momentum equation
After the cannonball is fired, the final momentum can be expressed as:
Final momentum=Momentum of cannon+Momentum of cannonball
This can be written as:
mc⋅vc+mb⋅vb
Where:
- vc is the recoil velocity of the cannon (which we need to find).
- vb=200m/s is the velocity of the cannonball.
Step 5: Set up the equation
Setting the initial momentum equal to the final momentum gives us:
0=mc⋅vc+mb⋅vb
Substituting the known values:
0=100⋅vc+1⋅200
Step 6: Solve for the recoil velocity of the cannon
Rearranging the equation to solve for vc:
100⋅vc=−200
vc=−200100=−2m/s
Step 7: Interpret the result
The negative sign indicates that the direction of the cannon's recoil velocity is opposite to the direction of the cannonball's velocity. Thus, the cannon will move at a velocity of 2m/s in the opposite direction to the cannonball.
Final Answer
The velocity of the cannon after firing the cannonball is 2m/s in the opposite direction.
---
We have a cannon of mass mc=100kg and a cannonball of mass mb=1kg. The cannonball is fired with a velocity vb=200m/s. The cannon is initially at rest.
According to the law of conservation of momentum, the total momentum before firing the cannonball must equal the total momentum after firing.
Since both the cannon and the cannonball are initially at rest, the initial momentum is:
After the cannonball is fired, the final momentum can be expressed as:
- vc is the recoil velocity of the cannon (which we need to find).
- vb=200m/s is the velocity of the cannonball.
Setting the initial momentum equal to the final momentum gives us:
Rearranging the equation to solve for vc:
The negative sign indicates that the direction of the cannon's recoil velocity is opposite to the direction of the cannonball's velocity. Thus, the cannon will move at a velocity of 2m/s in the opposite direction to the cannonball.
The velocity of the cannon after firing the cannonball is 2m/s in the opposite direction.
Topper's Solved these Questions
- LAWS OF MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:LAWS OF MOTIONExercise:ASSIGNMENT ( SECTION -A)
Explore 50 Videos
- LAWS OF MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:LAWS OF MOTIONExercise:ASSIGNMENT ( SECTION -B) objective type questions (one option is correct)
Explore 59 Videos
- LAWS OF MOTIONBook:AAKASH INSTITUTE ENGLISHChapter:LAWS OF MOTIONExercise:Illustration
Explore 7 Videos
- KINETIC THEORYBook:AAKASH INSTITUTE ENGLISHChapter:KINETIC THEORYExercise:EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
Explore 10 Videos
- MAGNETISM AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:MAGNETISM AND MATTER Exercise:ASSIGNMENT (SECTION D)
Explore 26 Videos
Similar Questions
A bullet of mass 0.1 kg is fired with a speed of 100 m/sec , the mass of gun is 50 kg . The velocity of recoil is
View SolutionA bullet of mass 0.1 kg is fired with a speed of 100 m/sec , the mass of gun is 50 kg . The velocity of recoil is
View SolutionA 0.66kg ball is moving wih a speed of 100m/s. The associated wavelength will be.
View SolutionWhat is the kinetic energy of a baseball (mass=0.15kg) moving with a speed of 20 m/s?
View SolutionA bullet of mass 10 g is fired from a gun of mass 1 kg with recoil velocity of gun 5 m/s. The muzzle velocity will be
View SolutionA canon of mass M is mounted on an east west frictionless railway track. The barrel of cannon faces the north east direction at an angle of 45∘ with the vertical. The canon fires a shot of mass M with a speed V relative to the barrel.
View SolutionA cannon of mass 1000kg located at the base of an inclined plane fires a shell of mass 50kg in horizontal direction with velocity 180km/h. The angle of inclination of the inclined plane with the horizontal is 45∘. The coefficient of friction between the cannon and inclined plane is 0.5. The maximum height, in metre, to which the cannon can ascend the inclined plane as a result of recoil is
View SolutionA man fires a bullet of mass 200 g at a speed of 5 m/s . The gun is of one kg mass. by what velocity the gun rebounds backwards
View SolutionA ball of mass 1kg is thrown up with an initial speed of 4m/s. A second ball of mass 2kg is released from rest from some height as shown in Fig. Choose the correct statement (s).
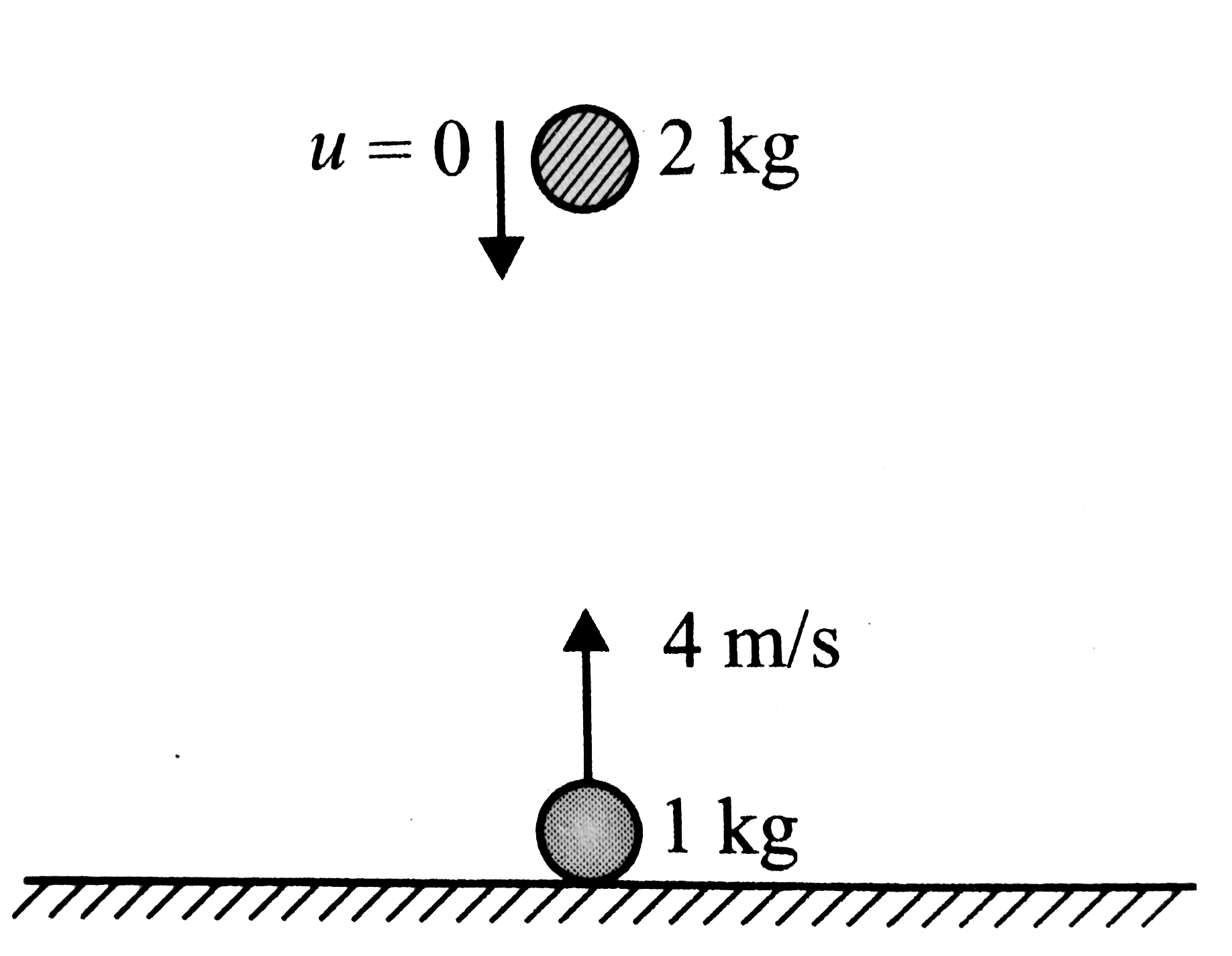
View SolutionFrom a rifle of mass 4kg, a bullet of mass 50g is fired with an initial velocity of 35m/s. Calculate the initial recoil velocity of the rifle.
View Solution
