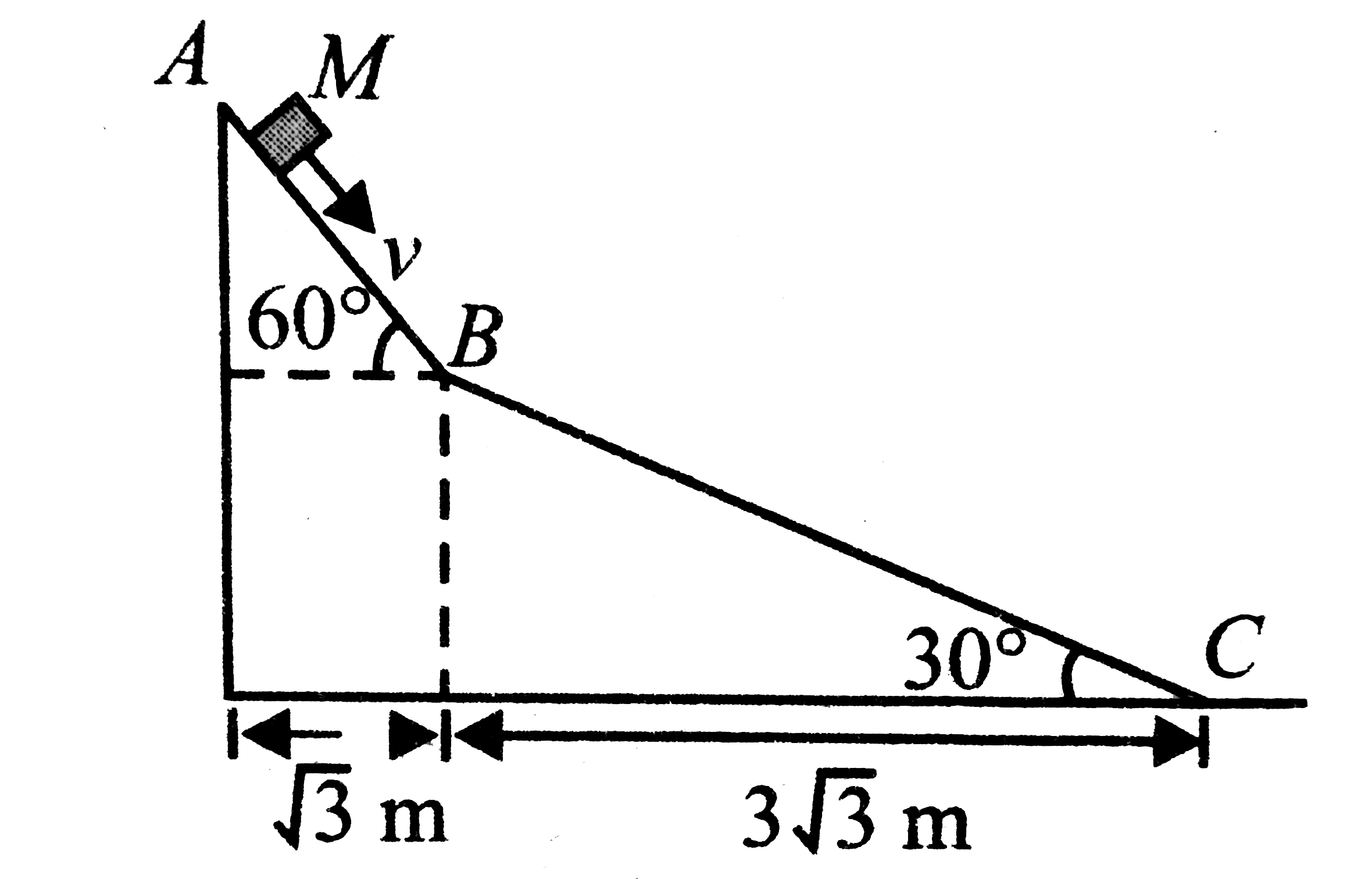
A small block of mass M moves on a frictionless surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘to30∘ at point B. The block is initially at rest at A. Assume that collisions between the block and the incline are totally inelastic
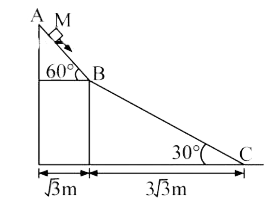
If collision between the block and the incline is completely elastic, then the vertical (upward) component of the velocity of the block at point B, immediately after it strikes the second incline is: ..
√120m/s
√105m/s
√30m/s
√75m/s
The correct Answer is:B
v2c=v2B+2g(h2−h1
⇒=vc=√452+2×10×3=√105ms−1
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A
20 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A small block of mass M move on a frictionless surface of an inclimed from as down is figure . The engle of the inclime suddenly change from 60∘ to 30∘ at point B . The block is initally at rest at A Assume the collsion between the block and the incline are totally inclassic (g=10m/s2)
If collision between the block and the incline is completely elestic , then the vartical (apward) component of the of the block at point B immediatly after it stricess the scond indine is -
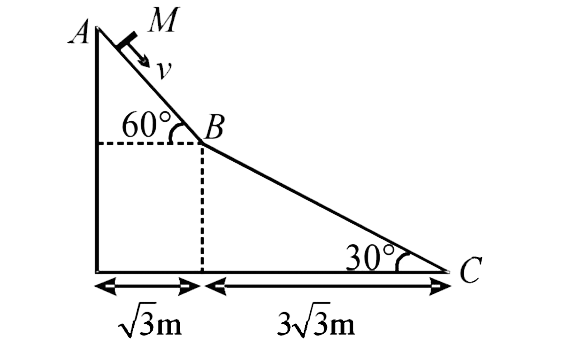
View SolutionA small block of mass M moves on a frictionless surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point B. The block is many at rest at A. Assume that collisions between the block id the incline are totally inelastic.
The speed of the block at point C, immediately before it leaves the second incline
View Solution
Knowledge Check
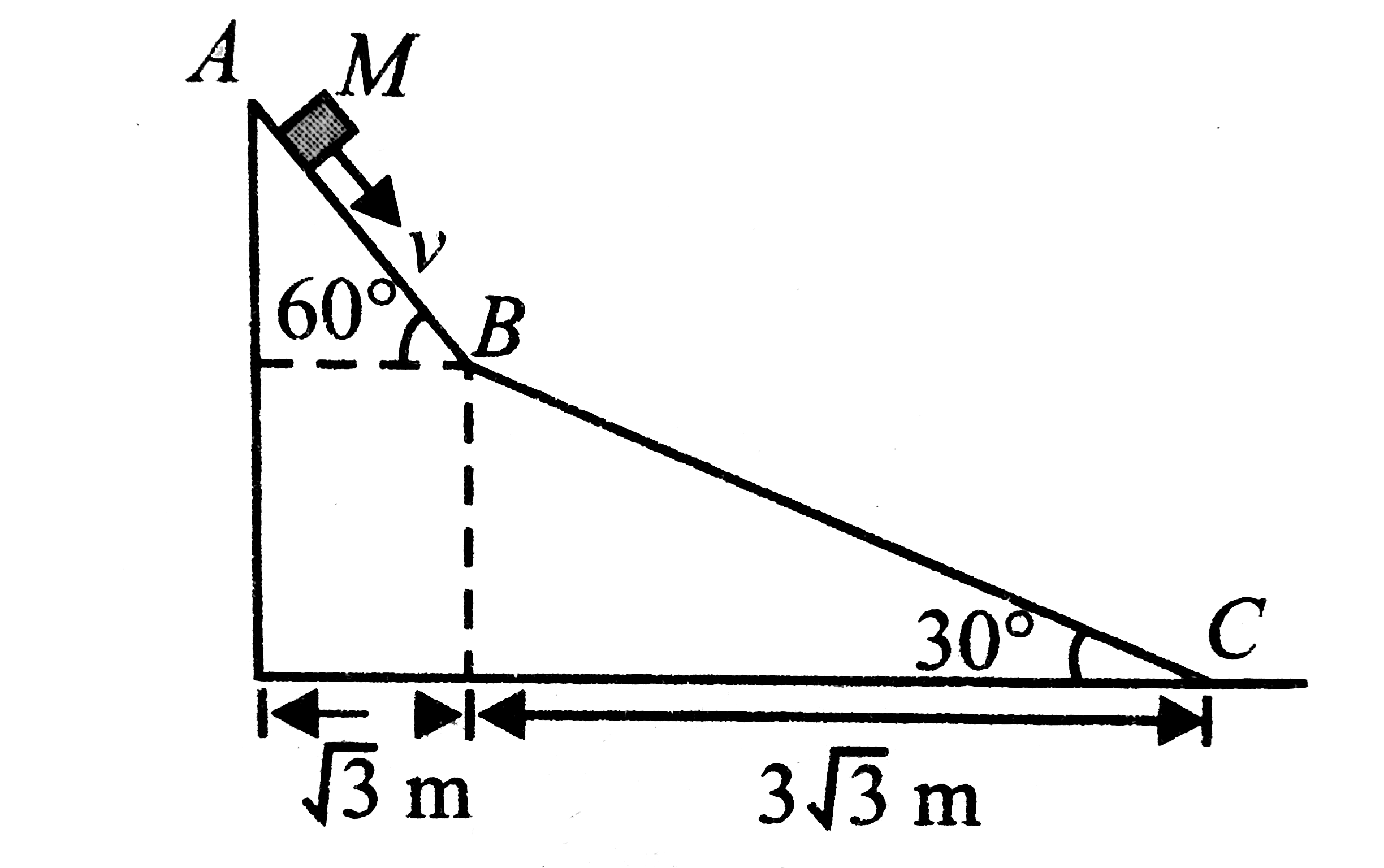
A small block of mass M moves on a frictionless surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point B. The block is many at rest at A. Assume that collisions between the block id the incline are totally inelastic.
The speed of the block at point B immediately after it strikes the second incline is
 A√60 m/sB√45 m/sC√30 m/sD√15 m/s
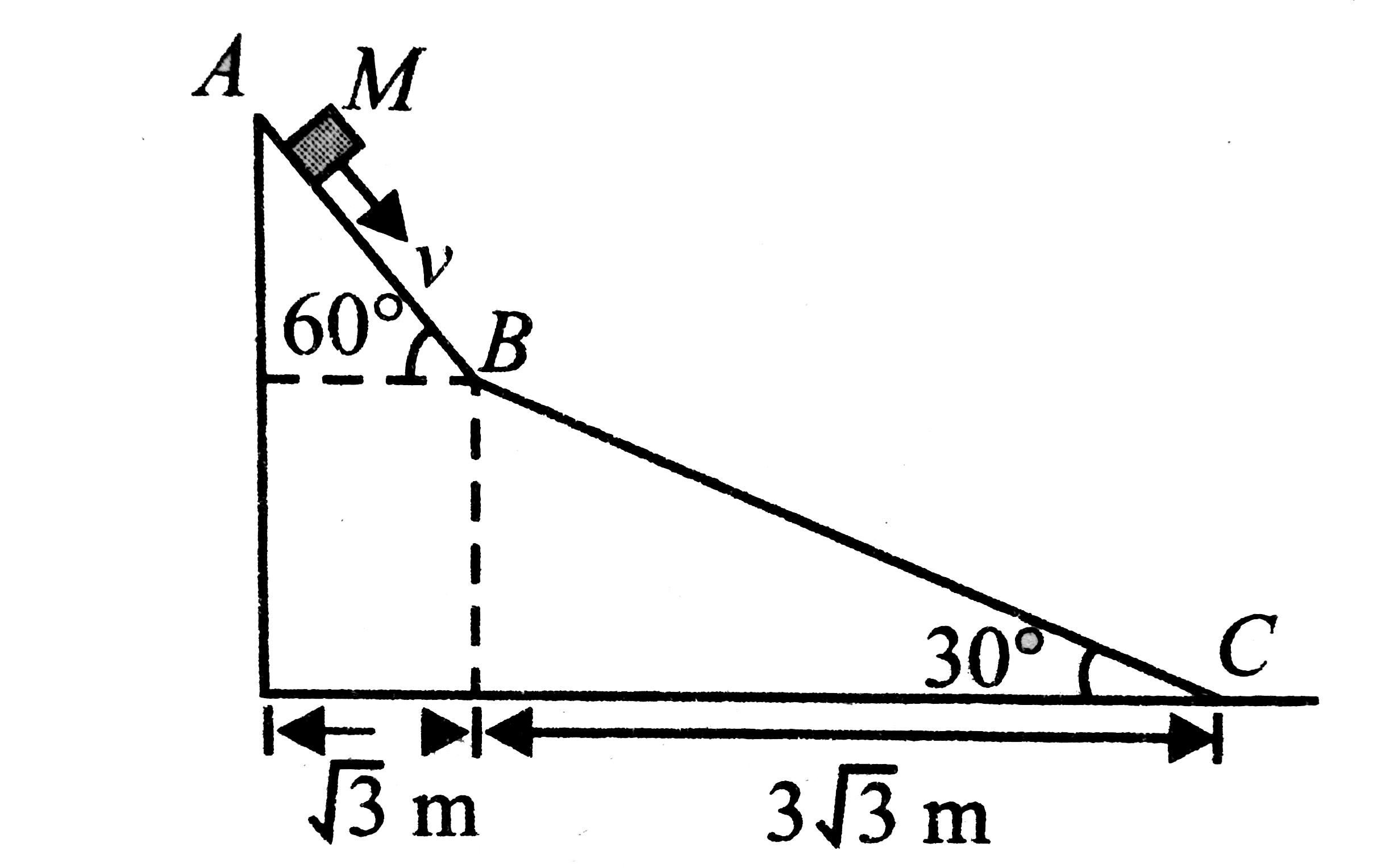
A√60 m/sB√45 m/sC√30 m/sD√15 m/sA small block of mass M moves on a friction-less surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point B. The block is initially at rest at A.
If collision between the block and the incline is completely elastic, then the vertical (upward) component of the velocity of the blocks at point B, immediately after it strikes the second incline is
 A√30 m/sB√15 m/sC0D−√15 m/s
A√30 m/sB√15 m/sC0D−√15 m/sTwo blocks each of mass M are resting on a frictionless inclined plane as shown in fig then:
 AThe block A moves down the planeBThe block B moves down the plane.CBoth the blocks remain at restDBoth the blocks move down the plane.
AThe block A moves down the planeBThe block B moves down the plane.CBoth the blocks remain at restDBoth the blocks move down the plane.
A block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is

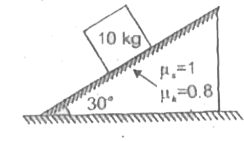
View SolutionA block of 10 kg mass is placed on a rough inclined surface as shown in figure. The acceleration of the block will be
View SolutionA block of mass 3kg is at rest on a rough inclined plan as shown in the Figure. The magnitude of net force exerted by the surface on the block will be

View SolutionA block of mass m is kept on an inclined plane is angle inclination θ(<ϕ), where ϕ= angle of friction. Then :

View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View Solution
