A cube is arranged such that its length, breadth and height are along X, Y and Z directions, One of its corners is situated a the origin. Length of each side of the cube is 25cm. The components of electric field are Ex=400√2N/C,Ey=0andEz=0 respectively. Find the flux coming out of the cube at one end.
25
25√2
25√2
zero
The correct Answer is:C
To find the electric flux coming out of one end of the cube, we can use Gauss's law, which states that the electric flux (Φ) through a surface is given by the product of the electric field (E) and the area (A) of the surface through which the field lines are passing. The formula for electric flux is:
Φ=E⋅A
1. Identify the dimensions of the cube:
The length of each side of the cube is given as 25 cm. Convert this to meters for consistency in SI units:
Side length=25 cm=0.25 m
2. Determine the area of one face of the cube:
Since the cube has square faces, the area A of one face is given by:
A=side2=(0.25 m)2=0.0625 m2
3. Identify the electric field components:
The components of the electric field are given as:
Ex=400√2 N/C,Ey=0,Ez=0
Since the electric field has no components in the y and z directions, we only consider Ex for the flux through the face normal to the x-axis.
4. Calculate the electric flux through the face normal to the x-axis:
The electric flux through the face of the cube that is normal to the x-axis can be calculated using the formula:
Φ=Ex⋅A
Substituting the values:
Φ=(400√2 N/C)⋅(0.0625 m2)
5. Perform the calculation:
First, calculate 400⋅0.0625:
400⋅0.0625=25
Now, multiply by √2:
Φ=25√2 Nm2/C
Final Answer:
The electric flux coming out of the cube at one end is:
Φ=25√2 Nm2/C
The length of each side of the cube is given as 25 cm. Convert this to meters for consistency in SI units:
Side length=25 cm=0.25 m
Since the cube has square faces, the area A of one face is given by:
A=side2=(0.25 m)2=0.0625 m2
The components of the electric field are given as:
Ex=400√2 N/C,Ey=0,Ez=0
Since the electric field has no components in the y and z directions, we only consider Ex for the flux through the face normal to the x-axis.
The electric flux through the face of the cube that is normal to the x-axis can be calculated using the formula:
Φ=Ex⋅A
Substituting the values:
Φ=(400√2 N/C)⋅(0.0625 m2)
First, calculate 400⋅0.0625:
400⋅0.0625=25
Now, multiply by √2:
Φ=25√2 Nm2/C
The electric flux coming out of the cube at one end is:
Φ=25√2 Nm2/C
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBook:AAKASH SERIESChapter:ELECTRIC CHARGES AND FIELDSExercise:Exercise-II
Explore 56 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:AAKASH SERIESChapter:DUAL NATURE OF RADIATION AND MATTERExercise:PRACTICE EXERCISEX
Explore 42 Videos
- ELECTRIC FIELD AND POTENTIALBook:AAKASH SERIESChapter:ELECTRIC FIELD AND POTENTIALExercise:PROBLEMS (LEVEL-II)
Explore 26 Videos
Similar Questions
Due to a charge inside a cube the electric field is Ex=600x1/2,Ey=0,Ez=0. The charge inside the cube is (approximately):

View SolutionA cube of side a is placed such that the nearest face , which is parallel to the yz plane , is at a distance a from the origin . The electric field components are
Ex=αx1/2,Ey=Ez=0.
The flux ϕE through the cube is

View SolutionA cube of side a is placed such that the nearest face , which is parallel to the yz plane , is at a distance a from the origin . The electric field components are
Ex=αx1/2,Ey=Ez=0.
The charge within the cube is

View SolutionFind the center of mass(x,y,z) of the following structure of four identical cubes if the length of each side of a cube is 1 unit.

View SolutionConsider the following conclusiond regarding the components of an electric field at a certain point in space given by Ex=−Ky,Ey=Kx,Ez=0 .
View SolutionThree thin rods each of length Land mass M are placed along x, y and z-axes such that one end of each rod is at origin. The moment of inertia of this system about z-axis is
View SolutionThe electric field components in the figure below are Ex=800x2N/C,Ey=Ez=0.
Calculate
(1) The flux throught he cube and
(2) The charge withing the cube
Assume that a =0.1 m
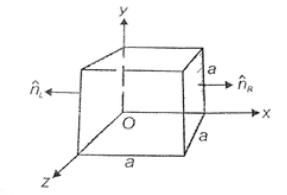
View SolutionAt each point on the surface of the cube shown in the figure, the electric field is parllel to the z- axis. The length of each edge of the cube is 3.0 m on the bottom face it is →E=34ˆkN/C and on the bottom face it is →E=20ˆkN/C . Find the net flux contained within the cube.
View SolutionThe electric components in the figure are Ex=αx1/2,Ey=0,Ez=0 where α=800N/m2 if a=0.1m is the side of cube then the charge with in the cube is
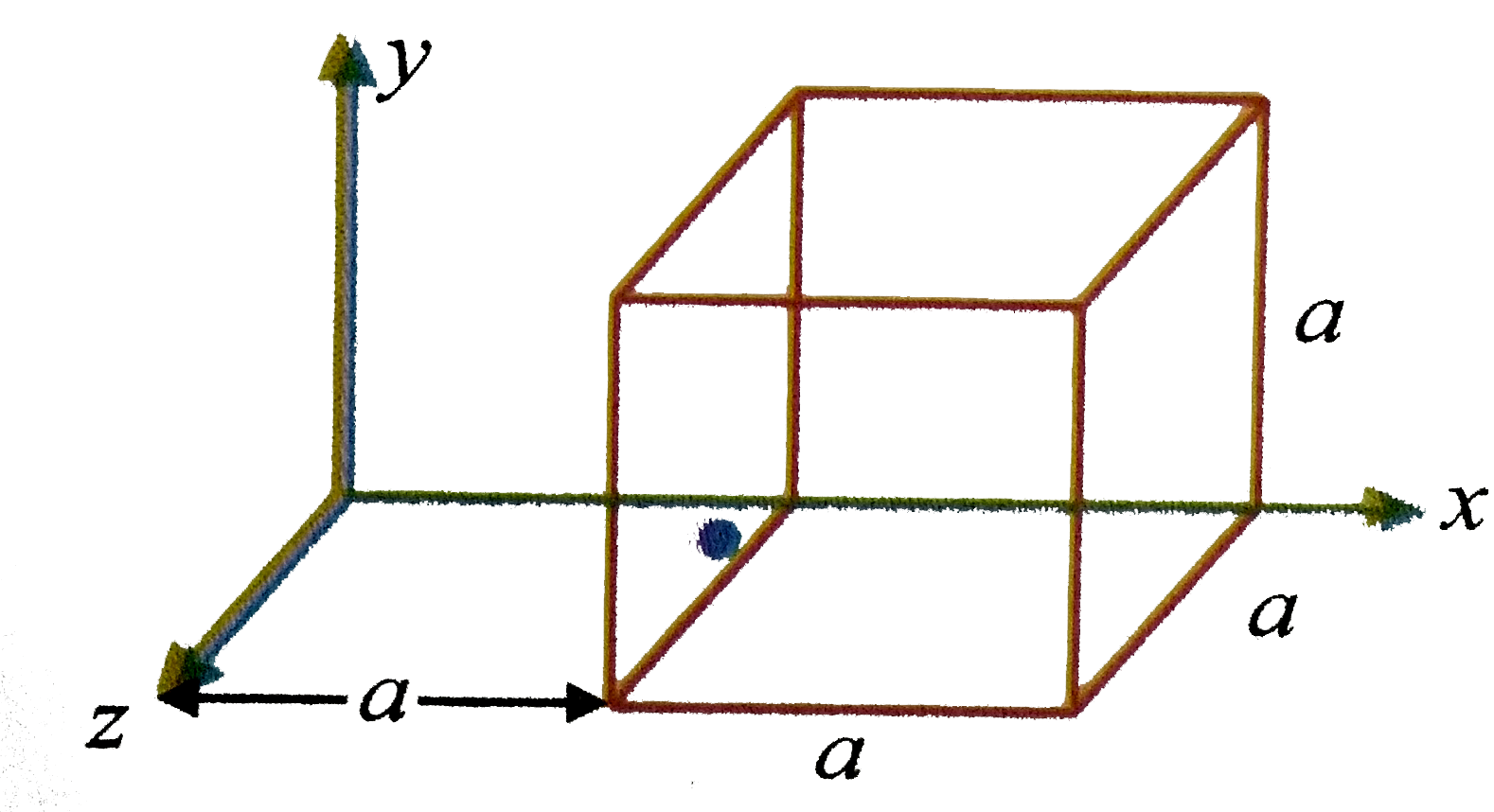
View SolutionThe length of each side of a cubical closed surface is L metre. If charge 48C is situated at one of the corners of the cube, Find the flux passing through the cube. (In Volt-metre)
View Solution