A charge of 8.85C is placed at the centre of a spherical Guassian surface of radius 5cm. The electric flux through the surface is
1012V/m
10−12V/m
108V/m
1010V/m
The correct Answer is:A
To find the electric flux through a spherical Gaussian surface surrounding a charge, we can use Gauss's Law. Here’s how to solve the problem step by step:
1. Identify the Given Values:
- Charge (Q) = 8.85 C
- Radius of the Gaussian surface (r) = 5 cm (this value is not directly needed for the calculation of electric flux)
2. Understand Gauss's Law:
Gauss's Law states that the electric flux (Φ) through a closed surface is proportional to the charge enclosed (Q) by that surface. Mathematically, it is expressed as:
Φ=Qϵ0
where ϵ0 is the permittivity of free space.
3. Use the Value of Permittivity:
The permittivity of free space (ϵ0) is approximately:
ϵ0=8.85×10−12C2/N m2
4. Calculate the Electric Flux:
Substitute the values into Gauss's Law:
Φ=8.85C8.85×10−12C2/N m2
Simplifying this gives:
Φ=1×1012N m2/C
Since 1N m2/C=1V m, we can express the flux as:
Φ=1012V m
5. Conclusion:
The electric flux through the surface is:
Φ=1012V m
Final Answer:
The electric flux through the surface is 1012V m.
---
- Charge (Q) = 8.85 C
- Radius of the Gaussian surface (r) = 5 cm (this value is not directly needed for the calculation of electric flux)
Gauss's Law states that the electric flux (Φ) through a closed surface is proportional to the charge enclosed (Q) by that surface. Mathematically, it is expressed as:
Φ=Qϵ0
where ϵ0 is the permittivity of free space.
The permittivity of free space (ϵ0) is approximately:
ϵ0=8.85×10−12C2/N m2
Substitute the values into Gauss's Law:
Φ=8.85C8.85×10−12C2/N m2
Simplifying this gives:
Φ=1×1012N m2/C
Since 1N m2/C=1V m, we can express the flux as:
Φ=1012V m
The electric flux through the surface is:
Φ=1012V m
The electric flux through the surface is 1012V m.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBook:AAKASH SERIESChapter:ELECTRIC CHARGES AND FIELDSExercise:Exercise-II
Explore 56 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:AAKASH SERIESChapter:DUAL NATURE OF RADIATION AND MATTERExercise:PRACTICE EXERCISEX
Explore 42 Videos
- ELECTRIC FIELD AND POTENTIALBook:AAKASH SERIESChapter:ELECTRIC FIELD AND POTENTIALExercise:PROBLEMS (LEVEL-II)
Explore 26 Videos
Similar Questions
A charge 10μC is placed at the centre of a hemisphere of radius R=10cm as shown. The electric flux through the hemisphere (in MKS units)is

View SolutionA charge 'Q' is placed at the centre of a hemispherical surface of radius 'R'. The flux of electric field due to charge 'Q' through the surface of hemisphere is
View Solution
Knowledge Check
A point charge 4μC is at the centre of a cubic Gaussian surface 10 cm on edge. Net electric flux through the surface is
A2.5×105Nm2C−1B4.5×105Nm2C−1C4.5×106Nm2C−1D2.5×106Nm2C−1
A point charge of 2.0μC is at center of a cublic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface?
View SolutionA surface encloses an electric dipole. The electric flux through the surface is
View SolutionA charge q is placed at the centre of the open end of a cylindrical vessel . The flux of the electric field through the surface of the vessel is

View SolutionA point charge is placed at the centre of spherical Gaussian surface. Is electric flux ϕE changed if
(a) The sphere is replaced by a cube of same or different volume ?
(b) The charge is moved off-centre in the original sphere, still remaining inside ?
( c ) The charge is moved just outside the original sphere ?
(d) A second charge is placed near the outside to the origianl sphere ?
(e) A second charge is placed inside the Gaussian surface ?
View SolutionA surface enclosed an electric dipole, the flux through the surface is -
View SolutionA point charge q is placed at a distance d from the centre of a circular disc of radius R. Find electric flux flowing through the disc due to that charge
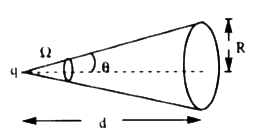
View SolutionA point charge q is placed at a distance a/2 directly above the centre of a square of side a. The electric flux through the square is
View Solution

