Three thin rods each of length Land mass M are placed along x, y and z-axes such that one end of each rod is at origin. The moment of inertia of this system about z-axis is
23ML2
4ML23
5ML23
ML23
The correct Answer is:A
To find the moment of inertia of the system of three thin rods about the z-axis, we can follow these steps:
Step 1: Understand the Configuration
We have three thin rods, each of length L and mass M. The rods are aligned along the x, y, and z-axes, with one end of each rod at the origin (0, 0, 0).
Step 2: Identify the Moment of Inertia for Each Rod
The moment of inertia I of a thin rod of mass M and length L about an axis through one end and perpendicular to its length is given by the formula:
I=13ML2
Step 3: Determine Which Rods Contribute to the Moment of Inertia About the z-axis
- The rod along the z-axis does not contribute to the moment of inertia about the z-axis because all its mass is located on the axis of rotation.
- The rods along the x-axis and y-axis will contribute to the moment of inertia about the z-axis.
Step 4: Calculate the Moment of Inertia for the Contributing Rods
- For the rod along the x-axis (let's call it I1):
I1=13ML2
- For the rod along the y-axis (let's call it I2):
I2=13ML2
Step 5: Sum the Contributions
The total moment of inertia Itotal about the z-axis is the sum of the moments of inertia of the rods along the x and y axes:
Itotal=I1+I2=13ML2+13ML2=23ML2
Step 6: Conclusion
Thus, the moment of inertia of the system about the z-axis is:
Itotal=23ML2
Final Answer
The correct option is 23ML2.
---
We have three thin rods, each of length L and mass M. The rods are aligned along the x, y, and z-axes, with one end of each rod at the origin (0, 0, 0).
The moment of inertia I of a thin rod of mass M and length L about an axis through one end and perpendicular to its length is given by the formula:
I=13ML2
- The rod along the z-axis does not contribute to the moment of inertia about the z-axis because all its mass is located on the axis of rotation.
- The rods along the x-axis and y-axis will contribute to the moment of inertia about the z-axis.
- For the rod along the x-axis (let's call it I1):
I1=13ML2
- For the rod along the y-axis (let's call it I2):
I2=13ML2
The total moment of inertia Itotal about the z-axis is the sum of the moments of inertia of the rods along the x and y axes:
Itotal=I1+I2=13ML2+13ML2=23ML2
Thus, the moment of inertia of the system about the z-axis is:
Itotal=23ML2
The correct option is 23ML2.
Topper's Solved these Questions
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:Check point 9.2
Explore 20 Videos
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:Check point 9.3
Explore 15 Videos
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Integer type q.
Explore 14 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
Similar Questions
Two rods of equal lengths(l) and equal mass M are kept along x and y axis respectively such that their centre of mass lie at origin. The moment of inertia about an line y = x, is
View SolutionA rod is placed along the line,y=2x with its centre at origin. The moment of inertia of the rod is maximum about.
View Solution
Knowledge Check
Three point masses each of mass m are placed at the corners of an equilateral triangle of side b. The moment of inertia of the system about an axis coinciding with one side of the triangle is
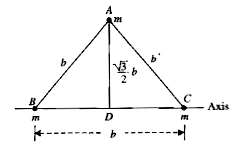 A3mb2Bmb2C(3/4)mb2D(2/3)mb2
A3mb2Bmb2C(3/4)mb2D(2/3)mb2
In the diagram shown below all three rods are of equal length L and equal mass M. The system is rotated such that rod B is the axis. What is the moment of inertia of the system ?

View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passing through its centre of mass and perpendicular to the plane of the particle.
View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passing through its centre of mass and perpendicular to the plane of the particle.
View SolutionThree rings each of mass M and radius R are arranged according to the figure. The moment of inertia of this system about an axis XX' on its plane would be

View SolutionThree uniform rods, each of length 21 ( = 1m) and mass M = 8 kg are rigidly joined at their ends to form a triangular framework. Find the moment of inertia of the framework about an axis passing through the midpoints of two of its sides?
View SolutionA non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is λ=λ0x. The distance of centre of mass of rod from the origin is :
View SolutionFour identical uniform thin rods, each of mass m and length l are joined to a common point O as shown in the figure. Moment of inertia of the system about an axis passing through O and lying in the plane of rods is
View Solution

