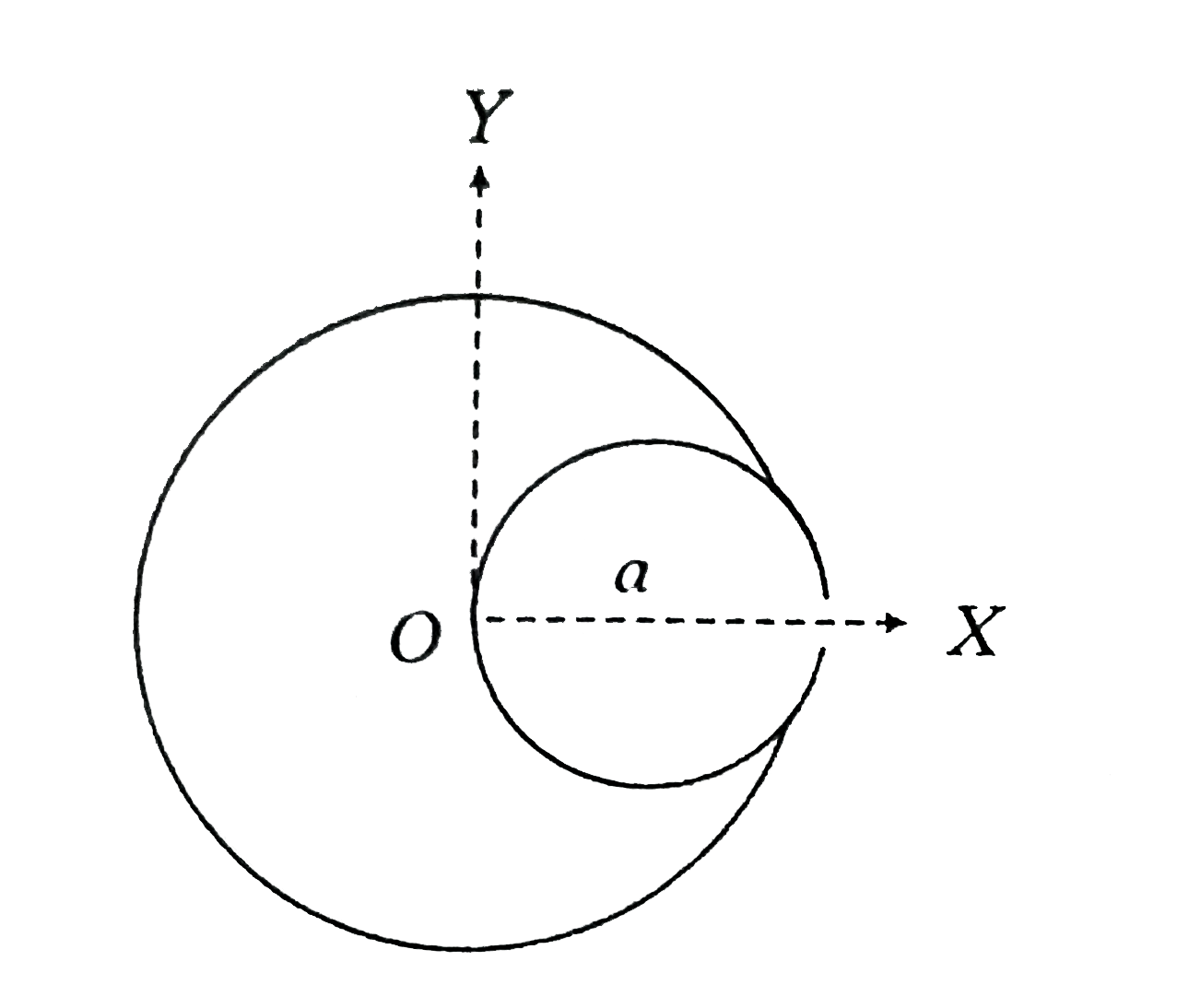Find the position of centre of mass of the uniform lamina shown in figure.
Video Solution
Text Solution
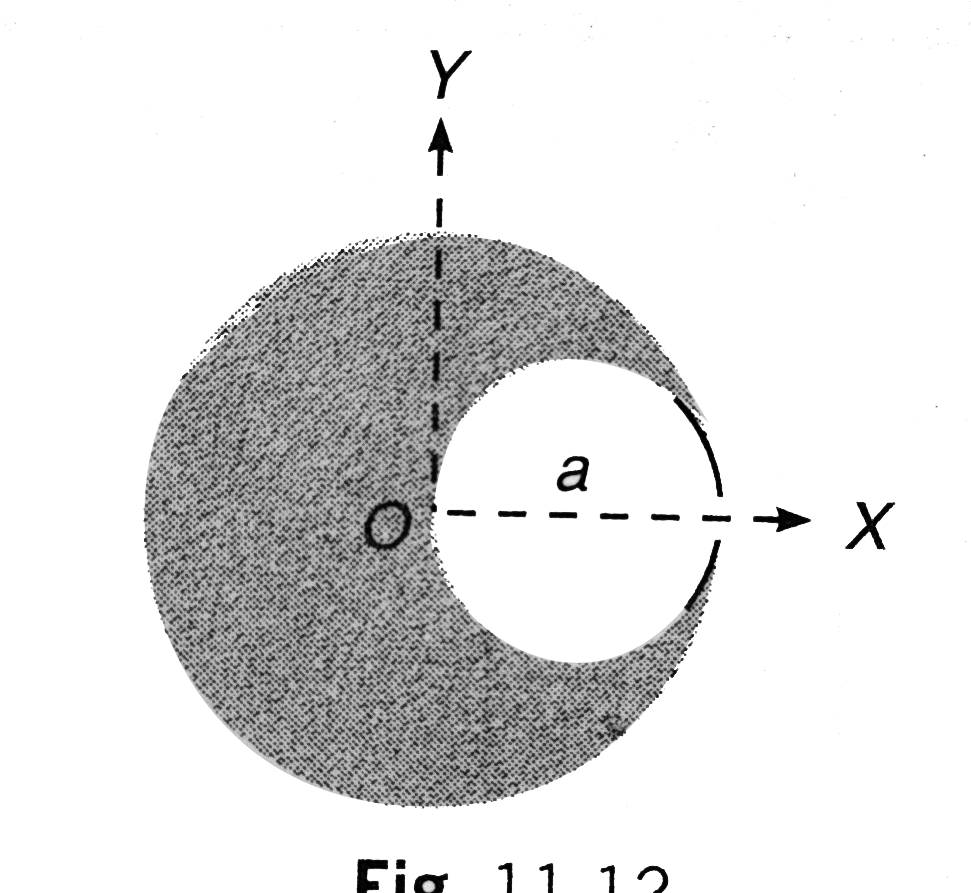
To find mass center of truncated bodies we can make use of superposition principle that is. If we add the removed portion in the same place we obtain the original body. The idea is illustrated in the following figure.

The removed portion is added to the trucated body keeping their location unchanged relative to the coordinate frame.
Denoting massses of the truncated body, removed portion and the original body by mtb,mrp and mob and location of their mass centres by xtb,xrp and xob, we can write mtbxtb+mrbxrp=mobxob
From the above equation we obtain position coordinate xtb of the mass center of the truncated body.
xtb=mobxob−mrbxrpmtb
Denoting mass per unit area by sigma, we can express the masses mtb,mrp and mob.
Mass of truncated body mtb=σ{π(r2−r24)}=3σπr24
Mass of the removed portion mrp=σπr24
Mass of the original body mob=σπr2
Mass center of the truncated body xtb
Mass center of the removed portion xrp=r2
Mass center of the original body xob=0
Substituting the above values in equation (1), we obtain the mass the center of the truncated body.
xtb=mobxob−mrbxrpmtb=(σπr2)×0−(σπr24)(r2)3σπr24=−r6
Mass center of the truncated body is at point (−r6,0)
|
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Knowledge Check
Which of the following points is the likely position of the centre of mass of the system shown in Fig.
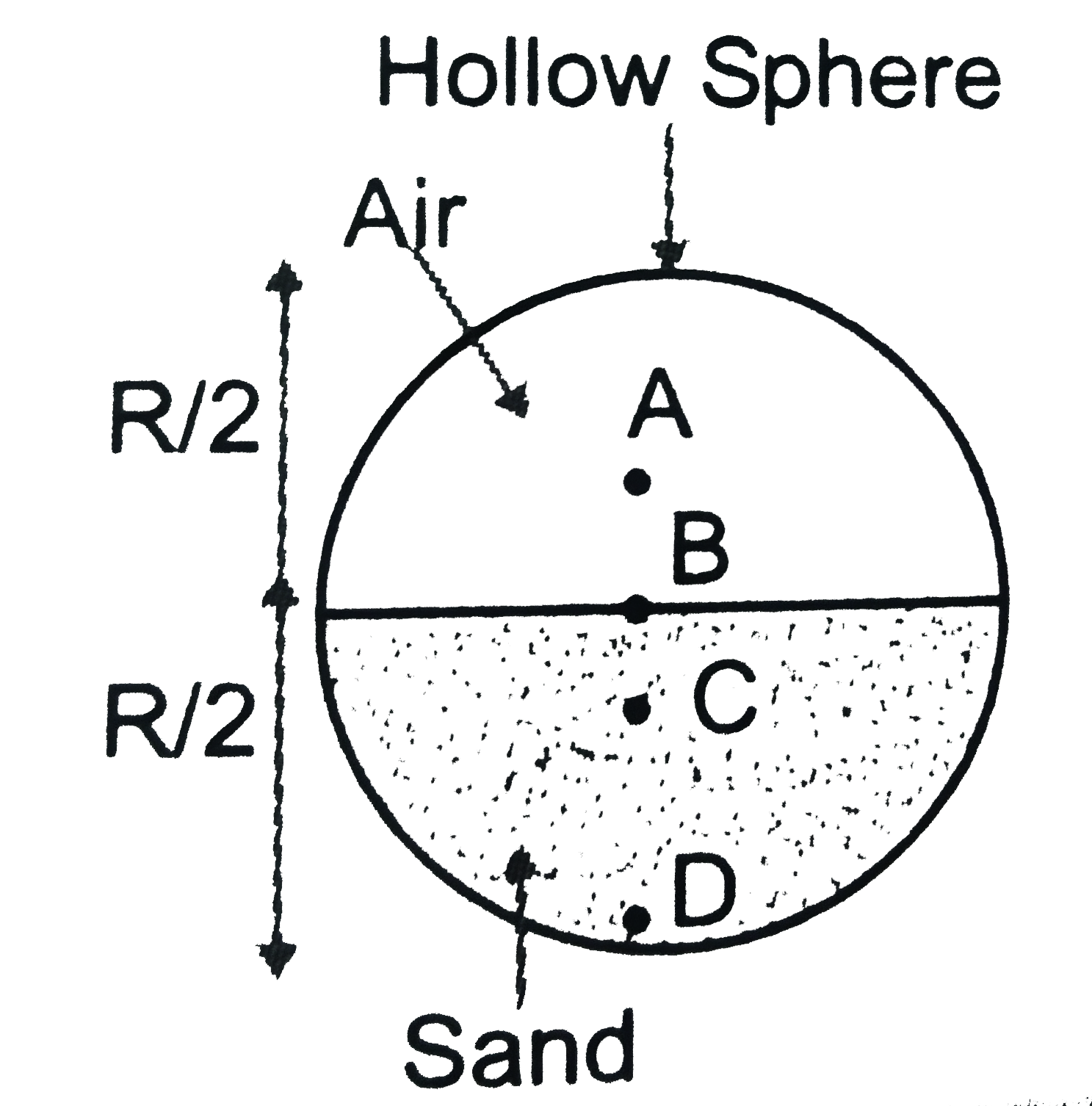 AABBCCDD
AABBCCDD
Find the co-ordinates of centre of mass of the lamina shown in figure
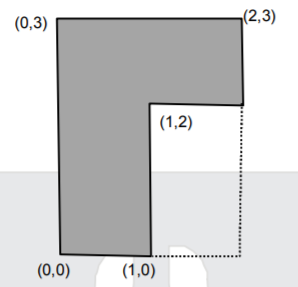
View SolutionFind the co-ordinates of centre of mass of the lamina shown in figure

View SolutionFind the x coordinate of the centre of mass of the bricks shown in figure :

View SolutionFind the centre of mass of a uniform solid cone.
View SolutionWhich of the following points is the likely position of the centre of mass of the system shown in Fig.

View SolutionWhich of the following points is the likely position of the centre of mass of the system shown in Fig.

View SolutionWhich of the following points is the likely position of the centre of mass of the system shown in Fig.

View Solution