Mass center of a system of a segment of a uniform circular rod(arc)
Find location of mass center of a thin uniform rod bent into shape of an arc.
To find the location of the center of mass of a thin uniform rod bent into the shape of an arc, we can follow these steps:
1. Define the Geometry of the Arc:
- Let the radius of the arc be r.
- The arc subtends an angle of 2θ at the center of the circle.
2. Identify the Mass per Unit Length:
- Let λ be the mass per unit length of the rod.
3. Set Up the Differential Element:
- Consider a small segment of the arc, which subtends an angle dα at the center.
- The length of this small segment dm can be expressed as:
dm=λ⋅r⋅dα
4. Determine the Coordinates:
- The x-coordinate of the center of mass can be expressed as:
xcm=∫xdmM
- For the arc, x can be represented as:
x=rcos(α)
5. Set Up the Integral:
- Since the arc is symmetric about the x-axis, the y-coordinate of the center of mass will be zero. Therefore, we only need to calculate xcm:
xcm=∫θ−θrcos(α)dmM
- Substituting dm:
xcm=∫θ−θrcos(α)⋅λrdαM
6. Calculate the Total Mass M:
- The total mass M of the arc is given by:
M=λ⋅r⋅(2θ)
7. Evaluate the Integral:
- Substitute dm into the integral:
xcm=r2λ∫θ−θcos(α)dαλ⋅r⋅(2θ)
- The integral ∫θ−θcos(α)dα evaluates to 2sin(θ):
xcm=r2λ⋅2sin(θ)λ⋅r⋅(2θ)
8. Simplify the Expression:
- Cancel out the common terms:
xcm=rsin(θ)θ
9. Conclusion:
- The center of mass of the arc is located at:
xcm=rsin(θ)θ
- Let the radius of the arc be r.
- The arc subtends an angle of 2θ at the center of the circle.
- Let λ be the mass per unit length of the rod.
- Consider a small segment of the arc, which subtends an angle dα at the center.
- The length of this small segment dm can be expressed as:
dm=λ⋅r⋅dα
- The x-coordinate of the center of mass can be expressed as:
xcm=∫xdmM
- For the arc, x can be represented as:
x=rcos(α)
- Since the arc is symmetric about the x-axis, the y-coordinate of the center of mass will be zero. Therefore, we only need to calculate xcm:
xcm=∫θ−θrcos(α)dmM
- Substituting dm:
xcm=∫θ−θrcos(α)⋅λrdαM
- The total mass M of the arc is given by:
M=λ⋅r⋅(2θ)
- Substitute dm into the integral:
xcm=r2λ∫θ−θcos(α)dαλ⋅r⋅(2θ)
- The integral ∫θ−θcos(α)dα evaluates to 2sin(θ):
xcm=r2λ⋅2sin(θ)λ⋅r⋅(2θ)
- Cancel out the common terms:
xcm=rsin(θ)θ
- The center of mass of the arc is located at:
xcm=rsin(θ)θ
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Mass Center of a sector of a uniform circular plate
Find location of mass center of a sector of a thin uniform plate.
View SolutionFind the velocity of center of mass of the system shown in the figure.

View SolutionThe coordinates of the center of mass of the following quarter circular arc are
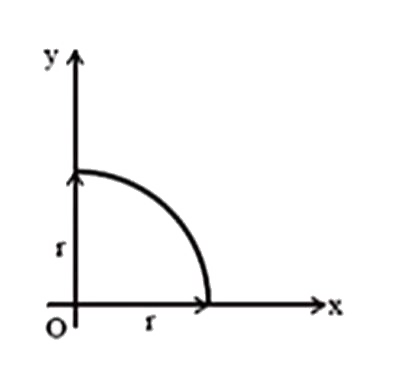
View SolutionFind the potential energy of the gravitational interation of a point mass of mass m and a thin uniform rod of mass M and length l, if they are located along a straight line such that the point mass is at a distance 'a' from one end. Also find the force of their interaction.
View SolutionFind coordinates of mass center of a uniform semicircular plate of radius r placed symmetric to the y-axis of a Cartesian coordinate system, with centre at origin.
View SolutionA particle placed
1.inside a uniform spherical shell of mass M, but not at the center
2.inside a uniform spherical shell of mass M, at the center
3.outside a uniform spherical shell of mass M, a distance r from the center
4.outside a uniform solid sphere of mass M, a distance 2r from the center
If F1,F2,F3 and F4 are gravitational forces acting on the particle in four cases.
View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to the rod.

View SolutionA mass m is at a distance a from one end of a uniform rod of length l and mass M. Find the gravitational force on the mass due to tke rod.

View SolutionThe distance of center of mass from the center of a uniform disc of radius R. if a circular plate is removed from the disc as shown in figure will be (C is centre of complete disc)
View SolutionFind out the moment of inertia of the circular arcs shown, each having mass M, radius R and having uniform mass distribution about an axis passing through the centre and perpendicular to the plane ?

View Solution
