A particle placed
1.inside a uniform spherical shell of mass M, but not at the center
2.inside a uniform spherical shell of mass M, at the center
3.outside a uniform spherical shell of mass M, a distance r from the center
4.outside a uniform solid sphere of mass M, a distance 2r from the center
If F1,F2,F3 and F4 are gravitational forces acting on the particle in four cases.
(a)F1>F2>F3>F4
(b)F1=F2<F3<F4
(c)F1=F2<F4<F3
(d)F1<F2<F3<F4
The correct Answer is:C
To solve the problem, we need to analyze the gravitational forces acting on a particle in four different scenarios involving a uniform spherical shell and a uniform solid sphere. Let's break down each case step by step.
Step 1: Analyze the first case (F1)
Case 1: A particle placed inside a uniform spherical shell of mass M, but not at the center.
According to the shell theorem, the gravitational force acting on a particle located inside a uniform spherical shell is zero, regardless of its position within the shell.
Conclusion:
F1=0
Step 2: Analyze the second case (F2)
Case 2: A particle placed inside a uniform spherical shell of mass M, at the center.
Again, by the shell theorem, the gravitational force acting on a particle at the center of a uniform spherical shell is also zero.
Conclusion:
F2=0
Step 3: Analyze the third case (F3)
Case 3: A particle placed outside a uniform spherical shell of mass M, at a distance r from the center.
For a particle outside a spherical shell, the gravitational force can be calculated using Newton's law of gravitation. The force is given by:
F3=GMmr2
where G is the gravitational constant, M is the mass of the shell, m is the mass of the particle, and r is the distance from the center of the shell.
Step 4: Analyze the fourth case (F4)
Case 4: A particle placed outside a uniform solid sphere of mass M, at a distance 2r from the center.
Using the same law of gravitation, the force acting on the particle at a distance 2r is:
F4=GMm(2r)2=GMm4r2
Step 5: Compare the forces
Now we can compare the forces F3 and F4:
- From the equations derived:
- F3=GMmr2
- F4=GMm4r2
Since F3 is greater than F4 because:
F3=4⋅F4
Final Conclusion
Now we can summarize the results:
- F1=0
- F2=0
- F3>F4
Thus, we can conclude:
F1=F2<F4<F3
Answer:
The correct option is that F1=F2 and F4<F3.
---
Case 1: A particle placed inside a uniform spherical shell of mass M, but not at the center.
F1=0
Case 2: A particle placed inside a uniform spherical shell of mass M, at the center.
F2=0
Case 3: A particle placed outside a uniform spherical shell of mass M, at a distance r from the center.
F3=GMmr2
where G is the gravitational constant, M is the mass of the shell, m is the mass of the particle, and r is the distance from the center of the shell.
Case 4: A particle placed outside a uniform solid sphere of mass M, at a distance 2r from the center.
F4=GMm(2r)2=GMm4r2
Now we can compare the forces F3 and F4:
- From the equations derived:
- F3=GMmr2
- F4=GMm4r2
F3=4⋅F4
Now we can summarize the results:
- F1=0
- F2=0
- F3>F4
F1=F2<F4<F3
The correct option is that F1=F2 and F4<F3.
Topper's Solved these Questions
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:Level-2
Explore 30 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Main (Archive)
Explore 43 Videos
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:LEVEL -0 Long Answer Type
Explore 3 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
- INTRODUCTION TO VECTORS & FORCES Book:VMC MODULES ENGLISHChapter:INTRODUCTION TO VECTORS & FORCES Exercise:JEE Advanced ( ARCHIVE LEVEL-2)
Explore 12 Videos
Similar Questions
Knowledge Check
A particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
AGMRB−GMRC−4GMRD−2GMR
A particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionThe electric field inside a spherical shell of uniform surface charge density is
View SolutionFigure shows a hemispherical shell of mass M and radius R and a concentric shell of mass m and radius 3R/4.

View SolutionA : The gravitational field intensity is zero everywhere inside a uniform spherical shell
R: The net force on a point mass inside a uniform spherical shell is zero everywhere .
View SolutionA uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
View SolutionA uniform metal sphere of radius a and mass M is surrounded by a thin uniform spherical shell of equal mass and redius 4a. The centre of the shell falls on the surface of the iner sphere
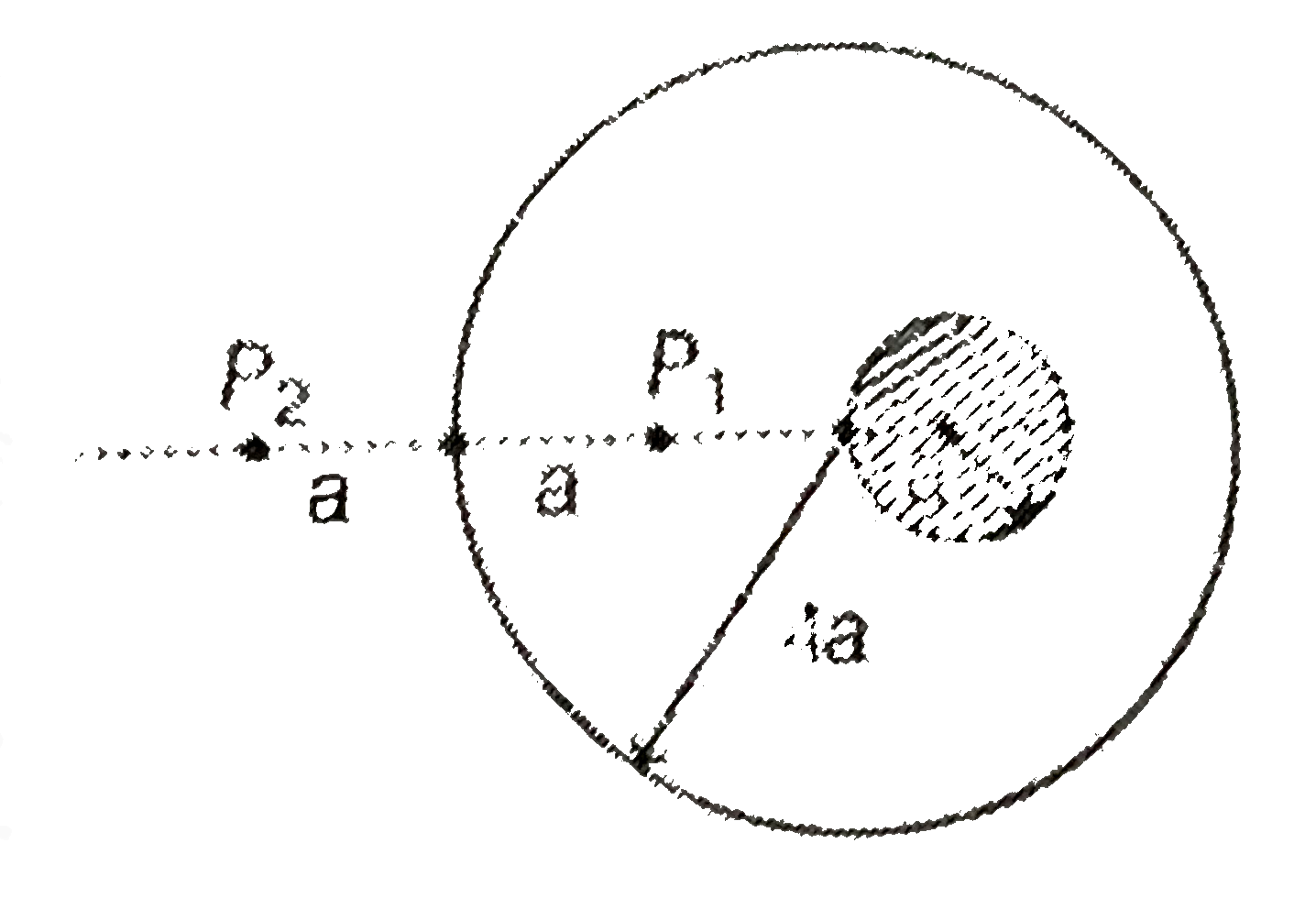
View Solution

