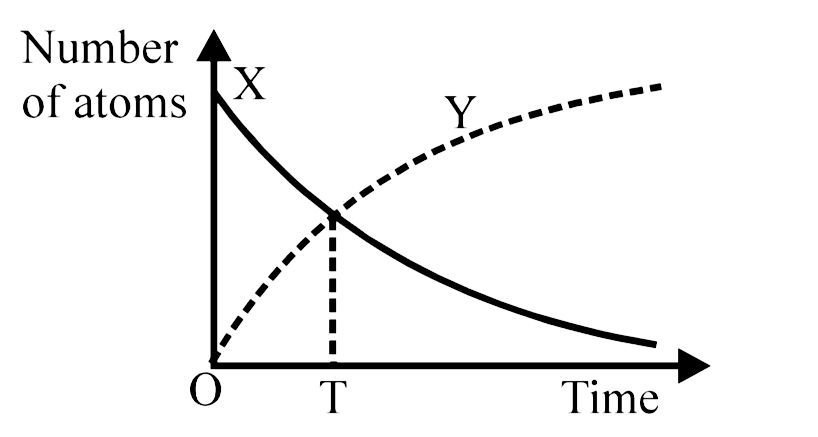
The graph represents the decay of a newly-prepared sample of radioactive nuclide X to a stable nuclide Y. The half-life of X is t. The growth curve for Y intersects the decay curve for X after time T. What is the time T ?
t/2
ln(t/2)
t
ln(2t)
The correct Answer is:C
At time T,N=N0−N⇒N=N02⇒T=t
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - Part-1 Physics
15 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physics
71 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 2
60 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
The half life of 2g sample of radioactive nuclide 'X' is 15 min. The half life time of 1g sample of X is
View SolutionThe half-life of a radioactive decay is x times its mean life. The value of zx is
View SolutionA radioactiev nuleus X deays to a stable nuleus Y. Then, time graph of rate of formation of Y against time t will be:
View SolutionThe relationship between decay constant λ and half-life T of a radioactive substance is
View SolutionThe half life of radioactive substance is T. Then the fraction of the substance that has decayed in time t is-
View SolutionIf T is the half-life of a radioactive material, then the fraction that would remain after a time T2 is
View SolutionA newly prepared radioactive nuclide has a decay constant λ of 10−6s−1. What is the approximate half-life of the nuclide?
View SolutionA radioactive elementX converts into another stable elemnet Y. Half-life of X is 2h. Initally, only X is present. After time t, the ratio of atoms of X and Y is found to be 1:4 Then t in hours is .
View SolutionRadioactive element decays to form a stable nuclide, then the rate of decay of reactant (dNdt) will vary with time (t) as shown in figure.
View SolutionCalculate the time taken to decay 100 percent of a radioactive sample in terms of (a) half- life T and
(b) mean-life Tav
View Solution
