One mole of an ideal gas undergoes a process whose molar heat capacity is 4R and in which work done by gas for small change in temperature is given by the relation dW=2RdT, then find the degree of freedom of gas
3
4
5
6
The correct Answer is:B
To solve the problem, we need to find the degree of freedom of the gas given the molar heat capacity and the work done during a small change in temperature. Let's break down the solution step by step.
Step 1: Understand the given information
We have:
- Molar heat capacity C=4R
- Work done by the gas for a small change in temperature dW=2RdT
- Number of moles n=1
Step 2: Use the first law of thermodynamics
The first law of thermodynamics states:
dQ=dU+dW
where dQ is the heat added to the system, dU is the change in internal energy, and dW is the work done by the system.
Step 3: Express dU in terms of Cv
For one mole of gas, the change in internal energy can be expressed as:
dU=nCvdT
Since n=1, we have:
dU=CvdT
Step 4: Substitute dQ and dW into the first law
From the given information, we can express dQ as:
dQ=CdT=4RdT
And from the work done:
dW=2RdT
Substituting these into the first law equation:
4RdT=CvdT+2RdT
Step 5: Simplify the equation
Now we can simplify the equation:
4RdT=CvdT+2RdT
Subtract 2RdT from both sides:
(4R−2R)dT=CvdT
This simplifies to:
2RdT=CvdT
Step 6: Solve for Cv
Since dT is not zero, we can divide both sides by dT:
Cv=2R
Step 7: Relate Cv to degrees of freedom
The molar heat capacity at constant volume Cv is related to the degrees of freedom f of the gas by the equation:
Cv=f2R
Substituting Cv=2R into this equation gives:
2R=f2R
Step 8: Solve for f
Dividing both sides by R (assuming R≠0):
2=f2
Multiplying both sides by 2:
f=4
Conclusion
The degree of freedom of the gas is f=4.
We have:
- Molar heat capacity C=4R
- Work done by the gas for a small change in temperature dW=2RdT
- Number of moles n=1
The first law of thermodynamics states:
dQ=dU+dW
where dQ is the heat added to the system, dU is the change in internal energy, and dW is the work done by the system.
For one mole of gas, the change in internal energy can be expressed as:
dU=nCvdT
Since n=1, we have:
dU=CvdT
From the given information, we can express dQ as:
dQ=CdT=4RdT
And from the work done:
dW=2RdT
4RdT=CvdT+2RdT
Now we can simplify the equation:
4RdT=CvdT+2RdT
Subtract 2RdT from both sides:
(4R−2R)dT=CvdT
This simplifies to:
2RdT=CvdT
Since dT is not zero, we can divide both sides by dT:
Cv=2R
The molar heat capacity at constant volume Cv is related to the degrees of freedom f of the gas by the equation:
Cv=f2R
Substituting Cv=2R into this equation gives:
2R=f2R
Dividing both sides by R (assuming R≠0):
2=f2
Multiplying both sides by 2:
f=4
The degree of freedom of the gas is f=4.
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - Part-1 Physics
15 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physics
71 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 2
60 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
One mole of an ideal gas undergoes a process whose molar heat capacity is 4R and in which work done by gas for small change in temperature is given by the relation dW=2RdT, then the ratio CPCV is
View SolutionOne mole of an ideal gas undergoes a process such that P∝1T. The molar heat capacity of this process is 4R.
View SolutionOne mole of an ideal gas undergoes a process T = 300 + 2V. Then amount of work done by gas when volume increases from 2m3 to 4m3:
View SolutionOne mole of an ideal diatomic gas is taken through a process whose P−V diagram is shown in the figure. The work done by the gas is
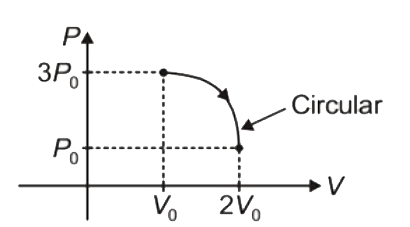
View Solutionn moles of an ideal gas undergo a process in which the temperature changes with volume as T=kv2. The work done by the gas as the temperature changes from T0 to 4T0 is
View SolutionOne mole of an ideal monatomic gas undergoes the process p=αT1/2, where α is a constant.
(a) Find the work done by the gas if its temperature increases by 50K.
(b) Also, find the molar specific heat of the gas.
View SolutionOne mole of an ideal monatomic gas undergoes the process p=αT1/2, where α is a constant.
(a) Find the work done by the gas if its temperature increases by 50K.
(b) Also, find the molar specific heat of the gas.
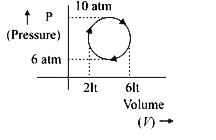
View SolutionAn ideal gas undergoes a cyclic process whose indicator diagram is as shown in the figure. Find the work done by the gas in 1 complete cycle.
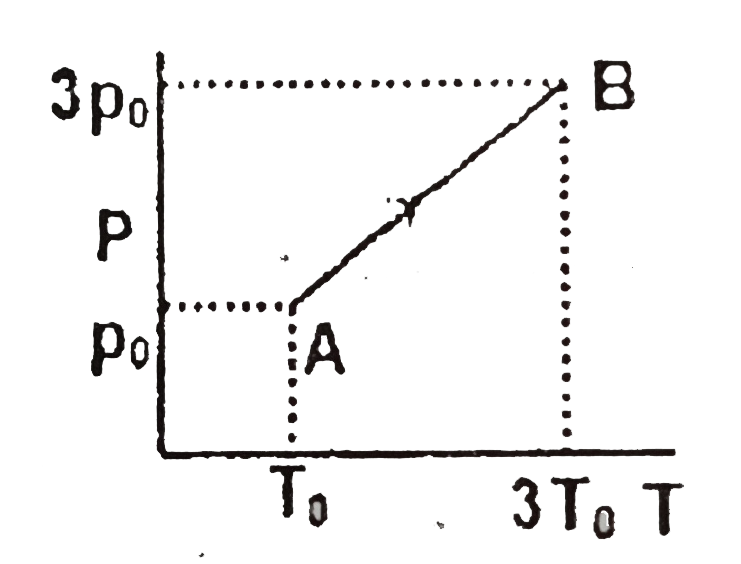
View SolutionTwo moles of a monoatomic ideal gas undergoes a process AB as shown in the figure. Then, find the work done during the process in Joule.
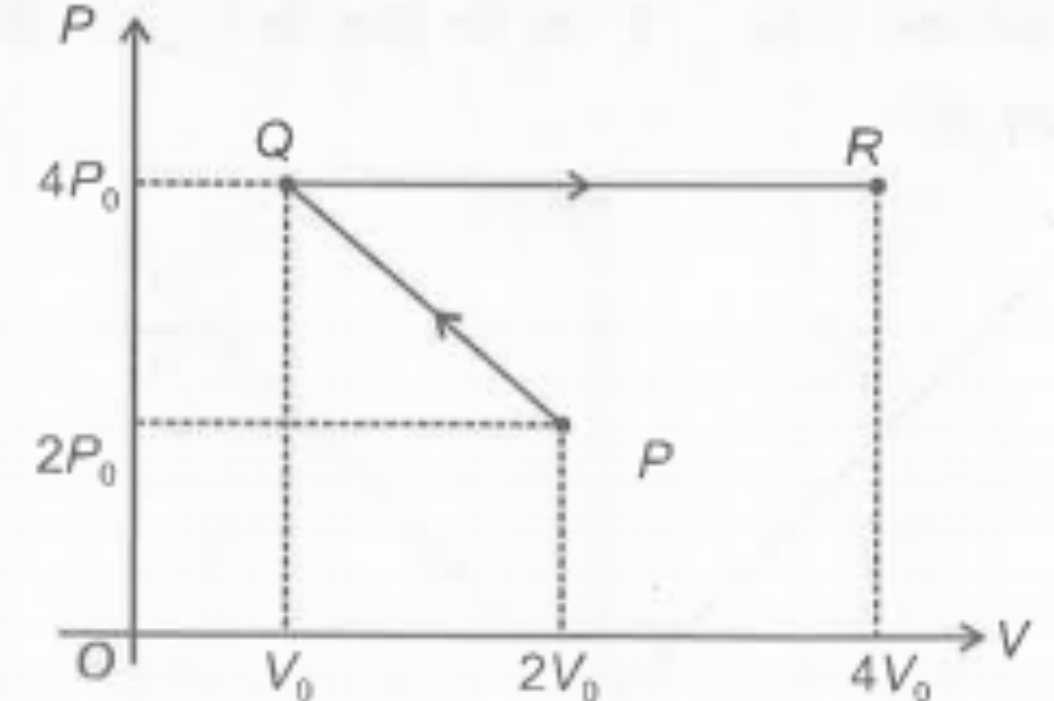
View SolutionAn ideal gas undergoes a process P→Q→R as shown in pressure (p) - volume (v) diagram.The work done by the gas is
View Solution
