One mole of an ideal gas undergoes a process T = 300 + 2V. Then amount of work done by gas when volume increases from 2m3 to 4m3:
300RIn2+4R
2 + 2 In 2
300 R In 2
None of these
The correct Answer is:A
To solve the problem of finding the work done by one mole of an ideal gas as it undergoes a specific process, we can follow these steps:
Step 1: Understand the Given Information
We are given:
- The process equation: T=300+2V
- The initial volume V1=2m3
- The final volume V2=4m3
- The number of moles n=1
Step 2: Use the Ideal Gas Law
The ideal gas law is given by:
PV=nRT
For one mole of gas (n=1), this simplifies to:
PV=RT
Substituting the expression for temperature T:
P=RTV=R(300+2V)V=300RV+2R
Step 3: Set Up the Work Done Integral
The work done W by the gas during expansion is given by:
W=∫V2V1PdV
Substituting the expression for P:
W=∫42(300RV+2R)dV
Step 4: Break Down the Integral
The integral can be split into two parts:
W=∫42300RVdV+∫422RdV
Step 5: Solve the First Integral
The first integral:
∫300RVdV=300RlnV
Evaluating from 2 to 4:
300R(ln4−ln2)=300Rln(42)=300Rln2
Step 6: Solve the Second Integral
The second integral:
∫2RdV=2RV
Evaluating from 2 to 4:
2R(4−2)=2R⋅2=4R
Step 7: Combine the Results
Combining both parts of the work done:
W=300Rln2+4R
Final Expression for Work Done
Thus, the total work done by the gas when the volume increases from 2m3 to 4m3 is:
W=300Rln2+4R
We are given:
- The process equation: T=300+2V
- The initial volume V1=2m3
- The final volume V2=4m3
- The number of moles n=1
The ideal gas law is given by:
PV=nRT
For one mole of gas (n=1), this simplifies to:
PV=RT
Substituting the expression for temperature T:
P=RTV=R(300+2V)V=300RV+2R
The work done W by the gas during expansion is given by:
W=∫V2V1PdV
Substituting the expression for P:
W=∫42(300RV+2R)dV
The integral can be split into two parts:
W=∫42300RVdV+∫422RdV
The first integral:
∫300RVdV=300RlnV
Evaluating from 2 to 4:
300R(ln4−ln2)=300Rln(42)=300Rln2
The second integral:
∫2RdV=2RV
Evaluating from 2 to 4:
2R(4−2)=2R⋅2=4R
Combining both parts of the work done:
W=300Rln2+4R
Thus, the total work done by the gas when the volume increases from 2m3 to 4m3 is:
W=300Rln2+4R
Topper's Solved these Questions
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE MAIN (ARCHIVE )
Explore 81 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:Level - 1
Explore 75 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
Explore 1 Video
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) TRUE/FALSE
Explore 1 Video
Similar Questions
One mole of an ideal gas whose adiabatic exponent is γ=43 undergoes a process P=200+1V . Then change in internal energy of gas when volume changes from 2m2 to 4m3 is:
View SolutionOne mole of ideal gas goes through processP=2V21+V2. Then change in temperature of gas when volume changes from V=1m2 to 2m2 is :
View Solution
Knowledge Check
An ideal gas undergoes cyclic process ABCDA as shown in given p−V diagram. The amount of work done by the gas is
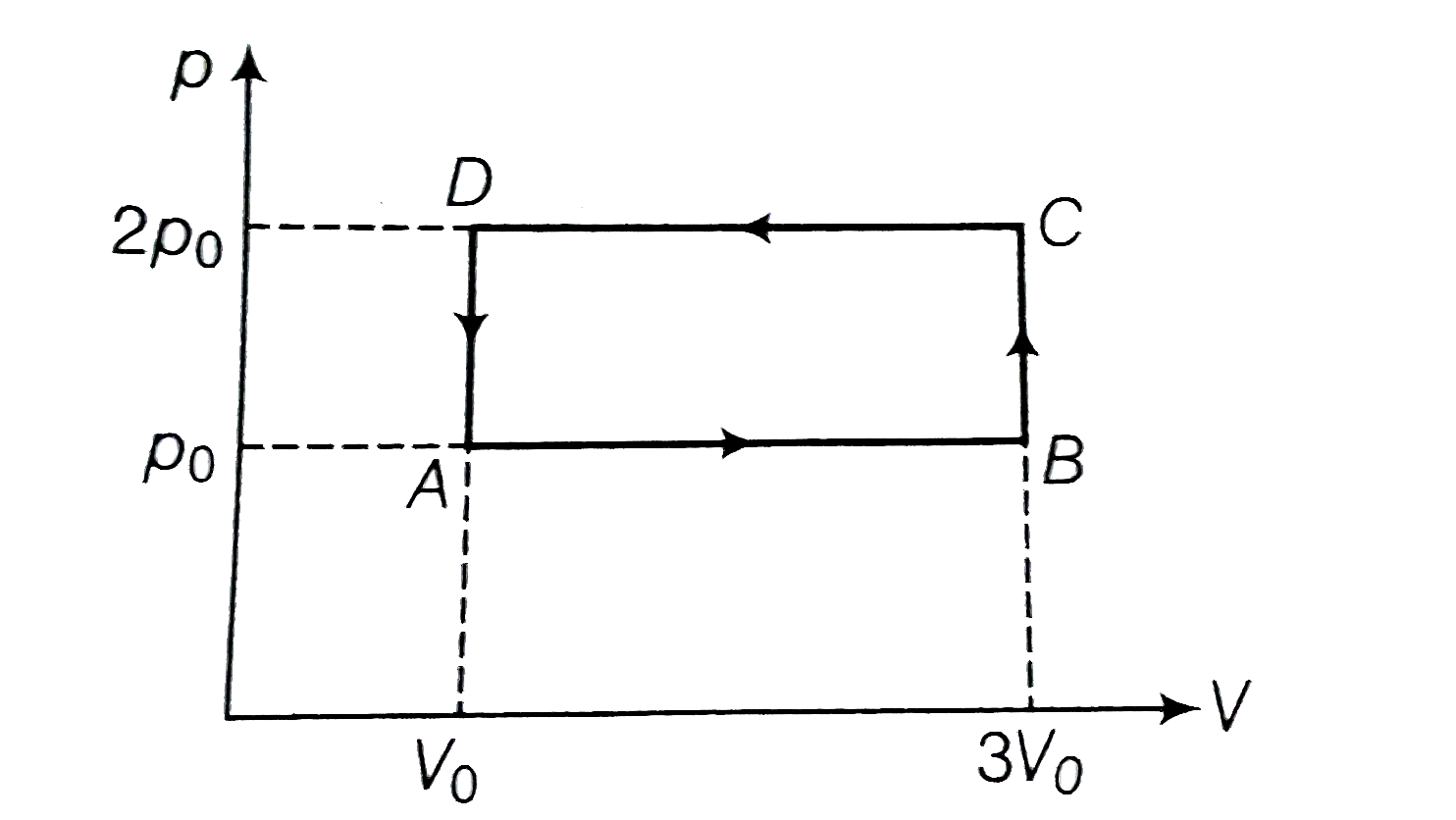 A6P0V0B−2P0V0C+2P0V0D+4P0V0
A6P0V0B−2P0V0C+2P0V0D+4P0V0One mole of an ideal gas undergoes a cyclic process ABCDA as shown in the P-V diagram, The net work done in the process is
(1 atm=10^(6) dyne cm^(-2)) A500 JB700 JC800 JD900 J
A500 JB700 JC800 JD900 JAn ideal gas system undergoes an isothermal process, then the work done during the process is
AnRTln(V2V1)BnRTln(V1V2)C2nRTln(V2V1)D2nRTln(V1V2)
An ideal gas undergoes cyclic process ABCDA as shown in givend p−V diagram. The amount of work done by the gas is

View SolutionOne mole of an ideal gas undergoes a process such that P∝1T. The molar heat capacity of this process is 4R.
View SolutionOne mole of an ideal gas undergoes a process whose molar heat capacity is 4R and in which work done by gas for small change in temperature is given by the relation dW=2RdT, then find the degree of freedom of gas
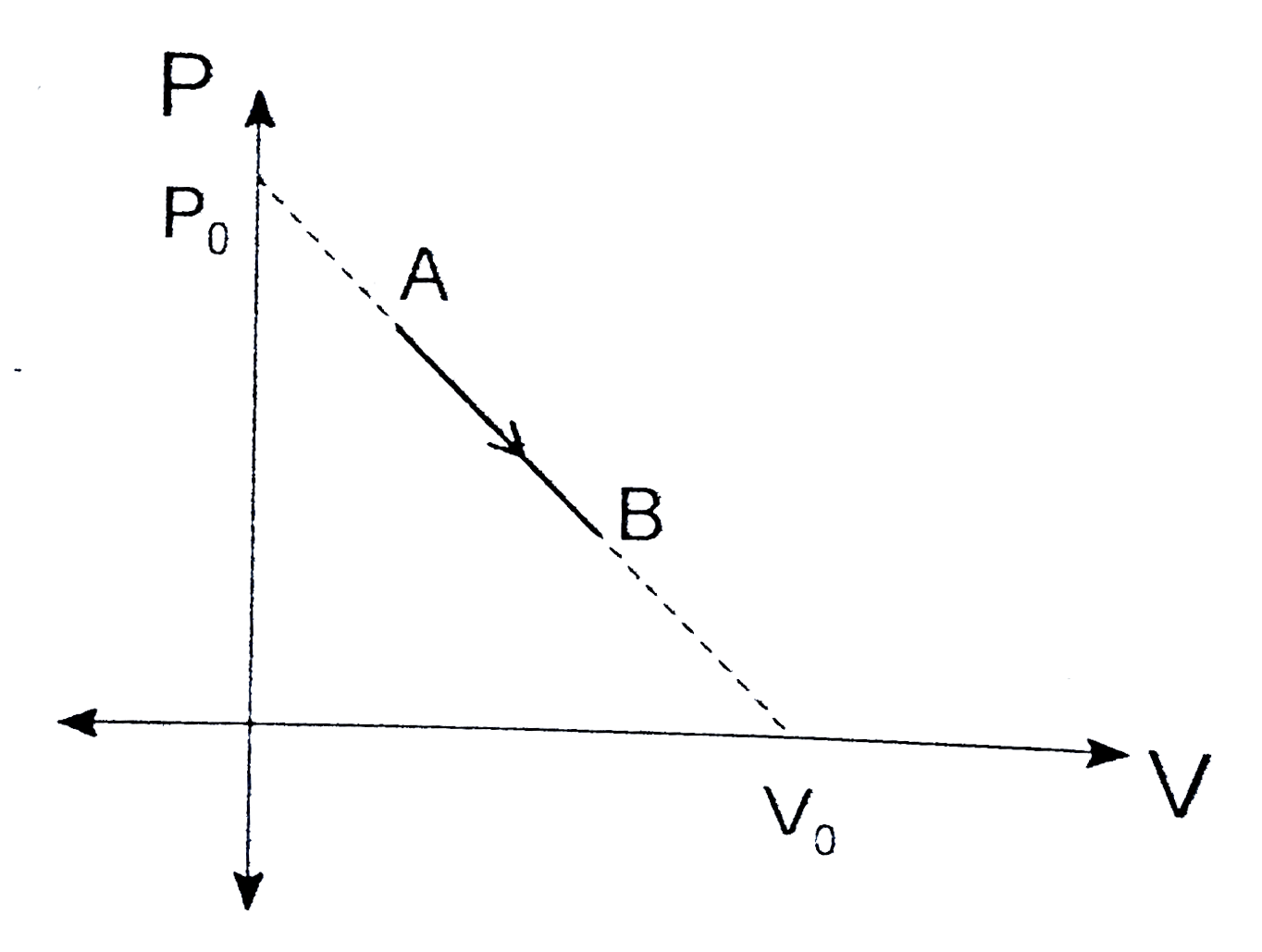
View SolutionOne mole of a monoatomic gas undergoes a linear process A→B in P−v diagram. The volume of the gas when the process turns from an endothermic to an exothermic one is
View SolutionOne mole of an ideal gas undergoes a process
P=P0−αV2
where α and P0 are positive constant and V is the volume of one mole of gas
Q. When temperature is maximum, volume is
View Solution

