One mole of an ideal gas whose adiabatic exponent is γ=43 undergoes a process P=200+1V . Then change in internal energy of gas when volume changes from 2m2 to 4m3 is:
400J
800J
1200J
None of these
The correct Answer is:C
To solve the problem, we need to calculate the change in internal energy of the gas as it undergoes a change in volume from 2m3 to 4m3. The process is defined by the equation P=200+1V, and we know the adiabatic exponent γ=43.
1. Identify the Given Values:
- Number of moles, n=1
- Adiabatic exponent, γ=43
- Initial volume, Vi=2m3
- Final volume, Vf=4m3
2. Calculate Initial Pressure Pi:
Pi=200+1Vi=200+12=200.5Pa
3. Calculate Final Pressure Pf:
Pf=200+1Vf=200+14=200.25Pa
4. Calculate Initial Temperature Ti using the Ideal Gas Law:
PV=nRT⟹Ti=PiVinR
Here, we need to express R in terms of Joules. For one mole of an ideal gas, R≈8.314J/(mol K):
Ti=200.5×21×8.314≈4018.314≈48.2K
5. Calculate Final Temperature Tf:
Tf=PfVfnR
Tf=200.25×41×8.314≈8018.314≈96.3K
6. Calculate Change in Temperature ΔT:
ΔT=Tf−Ti=96.3−48.2=48.1K
7. Calculate Cv (Specific Heat at Constant Volume):
Cv=Rγ−1=8.31443−1=8.31413=24.942J/(mol⋅K)
8. Calculate Change in Internal Energy ΔU:
ΔU=nCvΔT=1×24.942×48.1≈1200J
Final Answer:
The change in internal energy of the gas when the volume changes from 2m3 to 4m3 is approximately 1200J.
- Number of moles, n=1
- Adiabatic exponent, γ=43
- Initial volume, Vi=2m3
- Final volume, Vf=4m3
Pi=200+1Vi=200+12=200.5Pa
Pf=200+1Vf=200+14=200.25Pa
PV=nRT⟹Ti=PiVinR
Here, we need to express R in terms of Joules. For one mole of an ideal gas, R≈8.314J/(mol K):
Ti=200.5×21×8.314≈4018.314≈48.2K
Tf=PfVfnR
Tf=200.25×41×8.314≈8018.314≈96.3K
ΔT=Tf−Ti=96.3−48.2=48.1K
Cv=Rγ−1=8.31443−1=8.31413=24.942J/(mol⋅K)
ΔU=nCvΔT=1×24.942×48.1≈1200J
The change in internal energy of the gas when the volume changes from 2m3 to 4m3 is approximately 1200J.
Topper's Solved these Questions
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE MAIN (ARCHIVE )
Explore 81 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:Level - 1
Explore 75 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
Explore 1 Video
- GRAVITATIONBook:VMC MODULES ENGLISHChapter:GRAVITATIONExercise:JEE Advance (Archive) TRUE/FALSE
Explore 1 Video
Similar Questions
Knowledge Check
1 mole of an ideal gas at STP is subjected to a reversible adiabatic expansion to double its volume. Find the change in internal energy (γ=1.4)
A1169 JB769 JC1374 JD969 J
An ideal gas with adiabatic exponent γ=43 undergoes a process in which internal energy is related to volume as U=V2 . Then molar heat capacity of the gas for the process is :
View Solution0.5 moles of an ideal monoatomic gas undergoes a thermodynamic process from A to B as shown in figure. The change in internal energy of the gas during the process from A to B is
View SolutionAn ideal gas with adiabatic exponent (γ=1.5) undergoes a process in which work done by the gas is same as increase in internal energy of the gas. Here R is gas constant. The molar heat capacity C of gas for the process is:
View SolutionIf n moles of an ideal gas undergoes a thermodynamic process P=P0[1+(2V0V)2]−1, then change in temperature of the gas when volume is changed from V=V0 to V=2V0 is [Assume P0 and V0 are constants]
View SolutionOne mole of a gas absorbs 200 J of heat at constant volume. Its temperature rises from 298 K to 308 K. The change in internal energy is :-
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure,
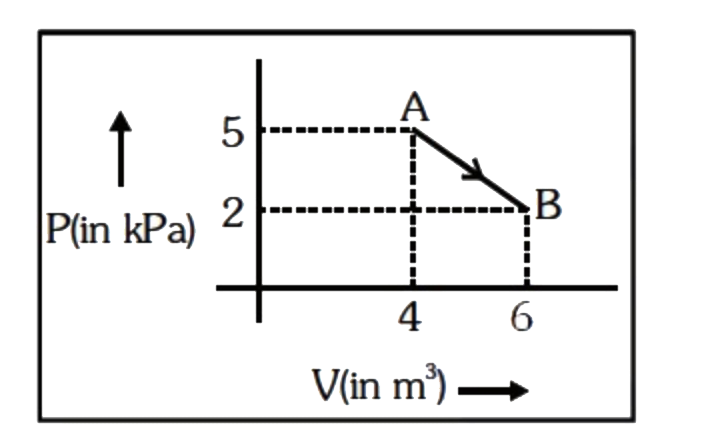
The change in internal energy of the gas during the transition is :
View SolutionOne mole of an ideal gas undergoes change of state from (4 L, 3 atm) to (6 L, 5 atm). If the change in internal energy is 45 L-atm then the change of enthalpy for the process is
View Solution

