n moles of an ideal triatomic linear gas undergoes a process in which the temperature changes with volume as k1V2 where k1 is a constant. Choose incorrect alternative.
At normal temperature Cv=52R
At any temperature Cp−Cv=R
At normal temperature molar heat capacity C=3R
At any temperature molar heat capacity C=3R
The correct Answer is:C
To solve the problem, we need to analyze the given statements about the ideal triatomic linear gas undergoing a process where the temperature varies with volume as T=k1V2. We will evaluate each statement to identify the incorrect one.
1. Understanding the Degrees of Freedom:
- For a triatomic linear gas, the degrees of freedom F is given by F=5 (3 translational + 2 rotational).
- Therefore, the molar heat capacity at constant volume Cv can be calculated as:
Cv=F2R=52R
2. Evaluating the First Statement:
- The first statement claims that at normal temperature, Cv=52R.
- Since we have calculated Cv as 52R, this statement is correct.
3. Evaluating the Second Statement:
- The second statement states that Cp−Cv=R.
- We know that for any ideal gas, this relation holds true. Thus:
Cp=Cv+R=52R+R=72R
- Therefore, Cp−Cv=R is also correct.
4. Evaluating the Third Statement:
- The third statement claims that at normal temperature, the molar heat capacity C=3R.
- We need to check if the molar heat capacity C can be derived from the process T=k1V2 and the ideal gas equation PV=nRT.
- Using the relation derived from the process and the ideal gas law, we find:
C=Cv+R=52R+R=72R
- This means that the statement claiming C=3R is incorrect.
5. Evaluating the Fourth Statement:
- The fourth statement claims that at any temperature, the molar heat capacity C=3R.
- Since we have established that C=72R at normal conditions and it does not hold for all temperatures, this statement is also incorrect.
Conclusion:
The incorrect statement is the third one, which states that at normal temperature, the molar heat capacity C=3R.
- For a triatomic linear gas, the degrees of freedom F is given by F=5 (3 translational + 2 rotational).
- Therefore, the molar heat capacity at constant volume Cv can be calculated as:
Cv=F2R=52R
- The first statement claims that at normal temperature, Cv=52R.
- Since we have calculated Cv as 52R, this statement is correct.
- The second statement states that Cp−Cv=R.
- We know that for any ideal gas, this relation holds true. Thus:
Cp=Cv+R=52R+R=72R
- Therefore, Cp−Cv=R is also correct.
- The third statement claims that at normal temperature, the molar heat capacity C=3R.
- We need to check if the molar heat capacity C can be derived from the process T=k1V2 and the ideal gas equation PV=nRT.
- Using the relation derived from the process and the ideal gas law, we find:
C=Cv+R=52R+R=72R
- This means that the statement claiming C=3R is incorrect.
- The fourth statement claims that at any temperature, the molar heat capacity C=3R.
- Since we have established that C=72R at normal conditions and it does not hold for all temperatures, this statement is also incorrect.
The incorrect statement is the third one, which states that at normal temperature, the molar heat capacity C=3R.
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - Part-1 Physics
15 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physics
71 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 2
60 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
n moles of an ideal gas undergo a process in which the temperature changes with volume as T=kv2. The work done by the gas as the temperature changes from T0 to 4T0 is
View SolutionAn ideal monatomic gas undergoes process PV1.25 = constant .Then
View SolutionWhich one of the following is correctly matched ?
View SolutionA gas undergoes a process in which its pressure P and volume V are related as VP = constant. The bulk modulus of gas for this process
View SolutionA gas undergoes a process in which its pressure P and volume V are related as VPn= constant. The bulk modulus of the gas in the process is:
View SolutionOne mole of an ideal monatomic gas undergoes a linear process from A to B , in which is pressure P and its volume V change as shown in figure .
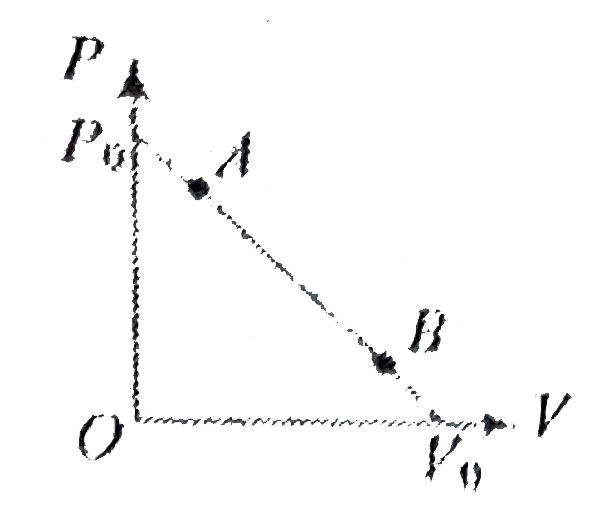
The absolute temperature T versus volume V for the given process is
View SolutionOne mole of an ideal monatomic gas undergoes a linear process from A to B , in which is pressure P and its volume V change as shown in figure .

The absolute temperature T versus volume V for the given process is
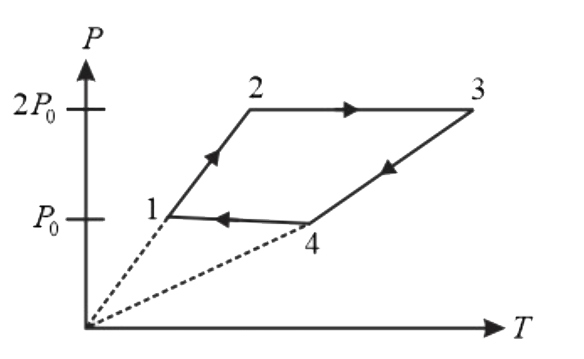
View SolutionOne mole of an ideal monoatomic gas undergoes a cyclic process, as shown in the figure. If the temperature of the gas at state 1 is 300 K and at state 4 is 500 K, then heat exchanged during process 2→3, is
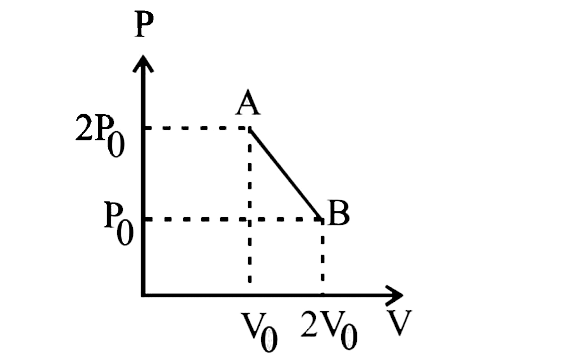
View Solutionn' moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will be:
View SolutionOne mole of an ideal monotomic gas undergoes a linear process from A to B in which its pressure p and its volume V change as shown in figure.

The maximum temperature of the gas during this process is
View Solution
