A newly prepared radioactive nuclide has a decay constant λ of 10−6s−1. What is the approximate half-life of the nuclide?
1hour
1day
1week
1month
The correct Answer is:c
To find the half-life of a radioactive nuclide given its decay constant (λ), we can use the formula:
T1/2=ln(2)λ
Where:
- T1/2 is the half-life,
- ln(2) is the natural logarithm of 2, approximately equal to 0.693,
- λ is the decay constant.
1. Identify the decay constant (λ):
Given that λ=10−6s−1.
2. Use the half-life formula:
Substitute the value of λ into the half-life formula:
T1/2=ln(2)10−6
3. Calculate ln(2):
We know that ln(2)≈0.693.
4. Substitute ln(2) into the formula:
T1/2=0.69310−6=0.693×106
5. Perform the multiplication:
T1/2≈693000s
6. Convert seconds to hours:
To convert seconds to hours, divide by 3600 (since there are 3600 seconds in an hour):
T1/2≈6930003600≈192.5hours
7. Convert hours to days:
To convert hours to days, divide by 24 (since there are 24 hours in a day):
T1/2≈192.524≈8.02days
8. Approximate to weeks:
Since 8.02 days is approximately one week, we conclude that the half-life of the nuclide is about one week.
Final Answer:
The approximate half-life of the nuclide is one week.
---
- T1/2 is the half-life,
- ln(2) is the natural logarithm of 2, approximately equal to 0.693,
- λ is the decay constant.
Given that λ=10−6s−1.
Substitute the value of λ into the half-life formula:
T1/2=ln(2)10−6
We know that ln(2)≈0.693.
T1/2=0.69310−6=0.693×106
T1/2≈693000s
To convert seconds to hours, divide by 3600 (since there are 3600 seconds in an hour):
T1/2≈6930003600≈192.5hours
To convert hours to days, divide by 24 (since there are 24 hours in a day):
T1/2≈192.524≈8.02days
Since 8.02 days is approximately one week, we conclude that the half-life of the nuclide is about one week.
The approximate half-life of the nuclide is one week.
Topper's Solved these Questions
- NUCLEAR PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:NUCLEAR PHYSICSExercise:Linked Comprehension
Explore 29 Videos
- NUCLEAR PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:NUCLEAR PHYSICSExercise:Integer
Explore 6 Videos
- NUCLEAR PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:NUCLEAR PHYSICSExercise:Subjective
Explore 35 Videos
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 5Exercise:Integer
Explore 12 Videos
- PHOTOELECTRIC EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:PHOTOELECTRIC EFFECTExercise:Integer Type
Explore 4 Videos
Similar Questions
The half life of a radio nuclide is 77 days then its decay constant is
View SolutionA radio nuclide A1 with decay constant λ1 transforms into a radio nuclide A2 with decay constant λ2. Assuming that at the initial moment, the preparation contained only the radio nuclide A1
(a) Find the equation decribing accumulation of radio nuclide A2 with time. (b) Find the time interval after which the activity of radio nuclide A2 reaches its maximum value.
View SolutionA radio nuclide A1 with decay constant λ1 transforms into a radio nuclide A2 with decay constant λ2. Assuming that at the initial moment, the preparation contained only the radio nuclide A1
(a) Find the equation describing accumulation of radio nuclide A2 with time. (b) Find the time interval after which the activity of ratio nucliei A2 reaches its maximum value.
View SolutionObtain a relation between half life of a radioactive substance and decay constant (λ) .
View SolutionThe half life of a radioactive substance is 13 years. The decay constant is
View SolutionA radioactive element undergoes two different types of radioactive disintegration, one with disintegration constant λ1 and the other with λ2. The half-life of the element is
View SolutionA radioactive substance contains 1015 atoms and has an activity of 6.0×1011 Bq. What is its half-life?
View SolutionNuclei of a radioactive element X are being produced at a constant rate K and this element decays to a stable nucleus Y with a decay constant λ and half-life T1/3. At the time t=0, there are N0nuclei of the element X.
The number NY of nuclei of Y at time t is .
View SolutionA radioactive nucleus X decays to a nucleus Y with a decay constant λX=0.1s−1, Y further decays to a stable nucleus Z with a decay constant
λY=1/30s−1. Initially, there are only X nuclei and their number is N0=1020. Set up the rate equations for the populations of X, Y and Z. The population of Y nucleus as a function of time is given by NY(t)={N0λX/(λX−λY)}[exp(−λYt)−exp(−λXt)].
Find the time at which NY is maximum and determine the population X and Z at that instant.
View SolutionThe graph represents the decay of a newly-prepared sample of radioactive nuclide X to a stable nuclide Y. The half-life of X is t. The growth curve for Y intersects the decay curve for X after time T. What is the time T ?
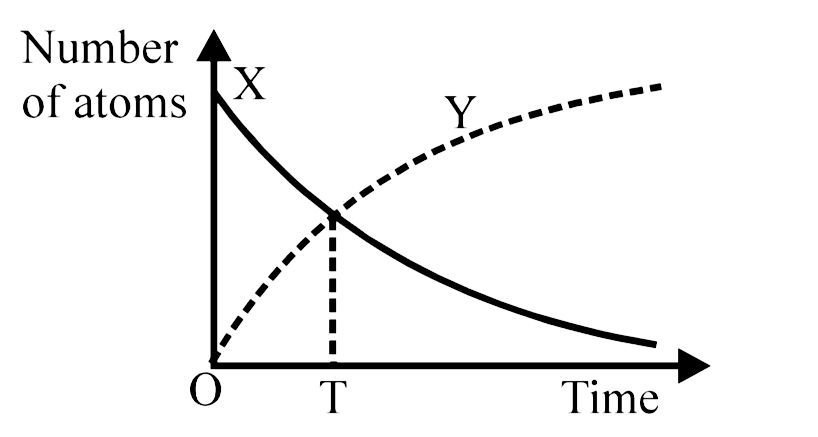
View Solution