A very long (length L) cylindrical galaxy is made of uniformly distributed mass and has radius R (R<<L) A star outside the galaxy is orbiting the galaxy in a plane perpendicular to the galaxy and passing through its centre. If the time period of star is T and its distance from the galaxy's axis is r, then-
T∝√r
T∝r
T∝r2
T2∝r3
The correct Answer is:B
To solve the problem, we need to find the relationship between the time period T of a star orbiting a long cylindrical galaxy and its distance r from the axis of the galaxy. We will use the principles of gravitation and centripetal motion.
1. Understanding the System:
- We have a long cylindrical galaxy of radius R and length L with uniformly distributed mass. A star is orbiting around this galaxy at a distance r from the axis.
2. Using Gauss's Law:
- To find the gravitational field g at the distance r from the axis of the cylinder, we can apply Gauss's law for gravitation. The gravitational field g is directed towards the center of the cylinder.
3. Setting Up the Gaussian Surface:
- Consider a cylindrical Gaussian surface of radius r and length L. The mass enclosed by this surface can be expressed in terms of the mass per unit length λ of the galaxy.
- The mass enclosed by the Gaussian surface is Menc=λL.
4. Calculating the Gravitational Field:
- According to Gauss's law:
∮g⋅dA=−Menc
- The area A of the curved surface of the cylinder is 2πrL. Thus, we have:
g⋅(2πrL)=−λL
- Rearranging gives:
g=−λ2πr
- Since g is directed inward, we can write:
g=2Gλr
- Here, G is the gravitational constant.
5. Relating Gravitational Force to Centripetal Force:
- The gravitational force acting on the star provides the necessary centripetal force for circular motion:
Fgravity=mg
- This force is equal to the centripetal force Fcentripetal=mv2r, where v is the orbital velocity of the star.
6. Expressing Velocity in Terms of Time Period:
- The velocity v can be expressed in terms of the time period T:
v=2πrT
- Substituting this into the centripetal force equation gives:
mg=m(2πr)2T2r
- Simplifying this leads to:
g=4π2rT2
7. Equating the Two Expressions for g:
- We have two expressions for g:
2Gλr=4π2rT2
- Rearranging gives:
T2=2π2r2Gλ
8. Conclusion:
- From the above relationship, we can see that T2 is proportional to r2:
T2∝r2⇒T∝r
Final Answer:
The time period T of the star is directly proportional to its distance r from the axis of the galaxy.
- We have a long cylindrical galaxy of radius R and length L with uniformly distributed mass. A star is orbiting around this galaxy at a distance r from the axis.
- To find the gravitational field g at the distance r from the axis of the cylinder, we can apply Gauss's law for gravitation. The gravitational field g is directed towards the center of the cylinder.
- Consider a cylindrical Gaussian surface of radius r and length L. The mass enclosed by this surface can be expressed in terms of the mass per unit length λ of the galaxy.
- The mass enclosed by the Gaussian surface is Menc=λL.
- According to Gauss's law:
∮g⋅dA=−Menc
- The area A of the curved surface of the cylinder is 2πrL. Thus, we have:
g⋅(2πrL)=−λL
- Rearranging gives:
g=−λ2πr
- Since g is directed inward, we can write:
g=2Gλr
- Here, G is the gravitational constant.
- The gravitational force acting on the star provides the necessary centripetal force for circular motion:
Fgravity=mg
- This force is equal to the centripetal force Fcentripetal=mv2r, where v is the orbital velocity of the star.
- The velocity v can be expressed in terms of the time period T:
v=2πrT
- Substituting this into the centripetal force equation gives:
mg=m(2πr)2T2r
- Simplifying this leads to:
g=4π2rT2
- We have two expressions for g:
2Gλr=4π2rT2
- Rearranging gives:
T2=2π2r2Gλ
- From the above relationship, we can see that T2 is proportional to r2:
T2∝r2⇒T∝r
The time period T of the star is directly proportional to its distance r from the axis of the galaxy.
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 5 B (Previous Year Questions)
9 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Illustration
34 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 4 B (Brain Storming Subjective Exercise)
20 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
Similar Questions

Calculate the moments of inertia of the figures shown, each having mass M, radius R and having uniform mass distribution about an axis perpendicular to the plane and passing through the centre?
View SolutionA charge q is uniformly distributed on a non-conducting disc of radius R. It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View Solution
Knowledge Check
One quarter sector is cut from a uniform circular disc of radius R. The sector has mass M. IT is made to rotate about a line perpendicular to its plane and passing through the centre of the original disc. Its moment of inertia about the axis of rotation is
AMR2/2BMR2/4CMR2/8D√2MR2Two thin discs each of mass M and radius r metre are attached to form a rigid body as shown in figure. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is
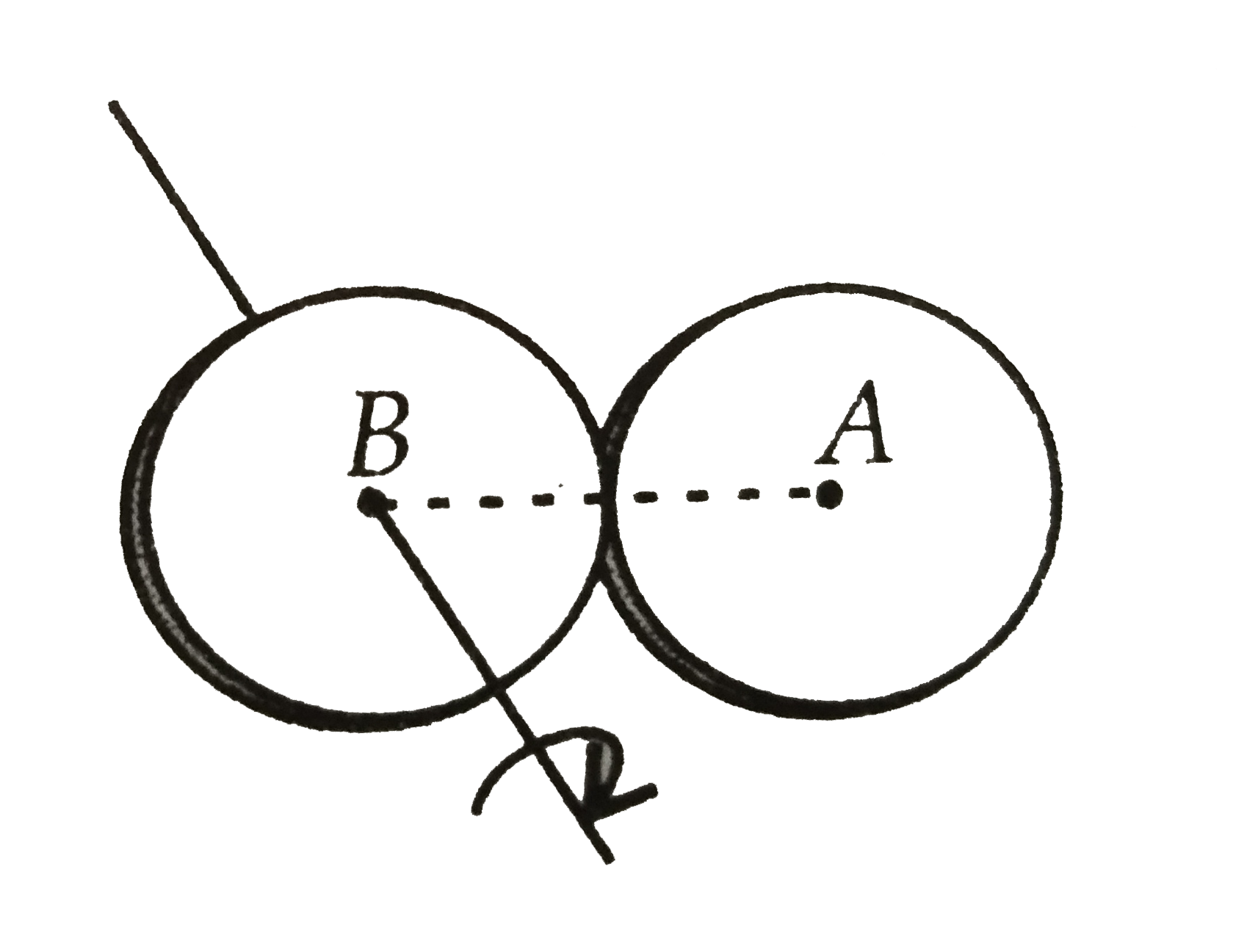 A2Mr2B3Mr2C4Mr2D5Mr2
A2Mr2B3Mr2C4Mr2D5Mr2
The radius of gyration of a uniform rod of length L about an axis passing through its centre of mass is
View SolutionOne quarter sector is cut from a uniform circular disc of radius R. This sector has mass M. It is made to rotate about a line perpendicular to its plane and passing through the centre of the original disc. It moment of inertia about the axis of rotation is.
 .
.
View SolutionFour thin rods of same mass and same length L form a square Radius of gyration of this system about an axis which is perpendicular to plane of square and passes through its centre is
View SolutionA uniform stick of length l is mounted so as to rotate about a horizontal axis perpendicular to the stick and at a distance d from the centre of mass. The time period of small oscillation has a minimum value when d/l is
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionThe radius of gyration of a uniform rod of mass m and length l about an axis perpendicular to its length and at distance l4 from its centre will be
View Solution
