From a solid sphere of mass M and radius R, a spherical portion of radius R2 is removed, as shown in the figure. Taking gravitational potential V=0 at r=∞, the potential at the centre of the cavity thus formed is (G=gravitational constant )

2−GM3R
−2GMR
−GM2R
−GMR
The correct Answer is:D
Step by step video & image solution for From a solid sphere of mass M and radius R, a spherical portion of radius ( R)/(2) is removed, as shown in the figure. Taking gravitational potential V=0 at r=oo, the potential at the centre of the cavity thus formed is (G=gravitational constant ) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:Exercise 5 B (Previous Year Questions)
Explore 9 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:Illustration
Explore 34 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:Exercise 4 B (Brain Storming Subjective Exercise)
Explore 20 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:subjective
Explore 14 Videos
- KINEMATICS-2DBook:ALLENChapter:KINEMATICS-2DExercise:Exercise (O-2)
Explore 46 Videos
Similar Questions
A sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionThe correct variation of gravitational potential V with radius r measured from the centre of earth of radius R is given by
View Solution
Knowledge Check
From a solid sphere of mass M and radius R, a spherical portion of radius R/2 is removed, as shown in the figure Taking gravitational potential V=0atr=∞, the potential at (G = gravitational constatn)
 A−2GM3RB−2GMRC−GM2RD−GMR
A−2GM3RB−2GMRC−GM2RD−GMR
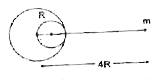
A particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ
View SolutionA spherical hole of radius R/2 is excavated from the asteroid of mass M as shown in the figure the gravitational acceleration at a point on the surface of the asteroid just above the excavation is

View SolutionA hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then

View SolutionA solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionA solid sphere having uniform charge density ρ and radius R is shown in figure. A spherical cavity ofradius R2 is made in it. What is the potential at point O?

View SolutionThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

View SolutionTwo spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
View Solution

