A hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then

xcm=−R/15
ycm=−R40
zcm=zero
None of these
The correct Answer is:A, B, C
xcm=43π(2R)30−23πR3R43π(2R)3−23πR3=−R15
ycm=43π(2R)30−23πR33R843π(2R)3−23πR3=−R40
zcm=0

Topper's Solved these Questions
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PHYSICS
Explore 784 Videos
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS SEC - 2
Explore 20 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCE ENGLISHChapter:TEST SERIESExercise:PHYSICS
Explore 130 Videos
Similar Questions
A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . They y -coordinate of the centre of mass of the remaining sphere is

View SolutionPositive charge is uniformly distrubuted with volume charge density ρ of sphere of radius R. A spherical cavity is created in the sphere as shown in figure. This electric field intensity inside the cavity at point P is(where CP =R/5 , C0C = 2R/3 , radius of cavity is R/4, C0 & C are centre of sphere & cavity respectively)
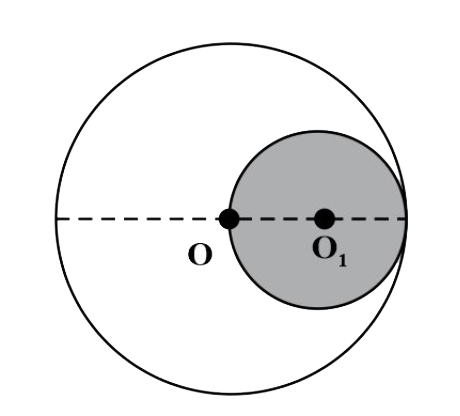
View SolutionA spherical cavity is made in a lead sphere of radius R such that its surface touches the outsides surface of lead sphere and passes through the centre. The shift in the centre of mass of the lead sphere as a result of this following, is
View SolutionA solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionA spherical hole is made in a solid sphere of radius R. The mass of the sphere before hollowing was M. The gravitational field at the centre of the hole due to the remaining mass is

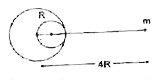
View SolutionA particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ
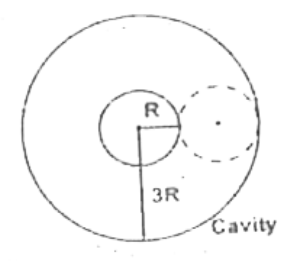
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionA solid sphere of radius R has a spherical cavity of radius r as shown in the figure. If the volume charge density σ is uniformly distributed over the whole volume of the sphere, then electric field strength at the centre of the sphere will be

View SolutionA thick shell with inner radius R and outer radius 3R has a uniform charge density σc/m3. It has a spherical cavity of radius R as shown in the figure. The electric field at the centre of the cavity is
View SolutionA point charge 'Q' is placed at the centre of a spherical cavity of radius 'b' carved inside a solid conducting sphere of radius 'a'. Then total energy of the system is:
[k=14π∈0]

View Solution

