State Gauss's theorem with the help of diagram, derive an expression for the electric field intensity due to uniformly charged thin spherical shell at a point outsideSolution in Punjabi
Gauss.s Theorem : It states that total electric flux through a closed surface is equal to 1ε0 times the magnitude of charge enclosed by it.
ϕ=∮→E.−→dS=qε0
Electric field due to uniformly charged spherical shell : Consider a spherical shell of radius R. .O. is the centre of the spherical shell ad + Q charge be uniformly distributed over the surface of the shell.
Let σ = Surface charge density
∴ Total charge on the shell = Q=σ(4πR2)
(i) →E at a point outside the shell :
Let P be a point outside the shell at a distance r (OP = r), where electric field intensity is to be determined. Draw a spherical Gaussian surface of radius r with centre at O. Consider a small area elements dS on this Gaussian surface
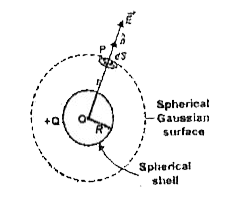
By symmetry consideration, the magnitude of →E is same at all points on this surface and direction is radially outward.
Now flux through area dS is given by
dϕE=→E.−→dS=→E.ˆndS
where ˆn is a unit vector normal to area dS
or dϕE=E(1)=dscos0∘
= E dS [∴ˆE∣∣ˆn,∴θ=θ]
Total flux through whole surface
ϕE=∮EdS
Using Gauss.s theorem,
ϕE=Qε0
From eqns, (2) and (3)
E∮dS=Qε0
[∴Area of Gaussian spherical surface=4πr2]
E(4πr2)=Qε0
⇒E=Q4πr2ε0=14πε0Qr2
which is also the expression for electric field due to a point charge It means that for a point lying outside the uniformaly charged spherical shell, the whole charged spherical shell behaves like a point charge.
Using eqn. (1) in eqn. (4), we have
E=14πε0σ(4πR2)r2
E=σR2ε0r2
(ii) →E at a point on the surface of shell (r = R) :
From eqn. (4), we get
E=Q4πε0R2
But Q=(4πR2)σ
∴E=(4πR2)4πε0R2=σε0orE=σε0
→E at a point inside the shell :
It the point P lies inside the shell at a distance r<R, then radius of Gaussian surface will be less than the radus of shell. Therefore, in thi case, Gaussian surface encloses no charge, i.e., q= 0 Using Gauss.s theorem,
∮→E.−→dS=qεon0=0
∴E=0
i.e., electric field intensity at all points inside a uniformly charged shell is zero.
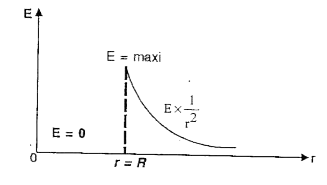
The variation of →E with distance from the centre of uniformly charged spherical shell is shown in fig. given below.
Topper's Solved these Questions
- GAUSS'S THEOREMBook:BETTER CHOICE PUBLICATIONChapter:GAUSS'S THEOREMExercise:MOST EXPECTED NUMERICALS
Explore 4 Videos
- GAUSS'S THEOREMBook:BETTER CHOICE PUBLICATIONChapter:GAUSS'S THEOREMExercise:SHORT ANSWER TYPE QUESTIONS
Explore 8 Videos
- FORCE ON A CURRENTBook:BETTER CHOICE PUBLICATIONChapter:FORCE ON A CURRENTExercise:NUMERICAL PROBLEMS
Explore 10 Videos
- HUYGENS' PRINCIPLEBook:BETTER CHOICE PUBLICATIONChapter:HUYGENS' PRINCIPLEExercise:LONG ANSWER TYPE QUESTIONS
Explore 11 Videos
Similar Questions
A box encloses an electric dipole of 3μCand−3C, if the dipole length is 6 cm, then find total electric flux associated with box.
View SolutionWhat is the use of Gaussian surface in electrostatics ?
View SolutionA currentof 5.0 A is flowing in eah of the two parallel conductors of infinite length separated by certain distance apart in vacuum in the same directions. Each conductor expereinces a force of 2×10−4Nm−1 due to the other. Find the separation between the two conductors.
View SolutionState Huygen's principle of propagation of light and prove the laws (Snell's law) of refraction on its basis.
View SolutionState Gauss's law. Derive an expression for electric intensity at a point outside the uniformly charged shell.
View SolutionDerive an expression for electric intensity E due to a uniformly charged thin spherical shell at a point outside the shell.
View SolutionFind expression for electric field intensity due to a uniformly charged thin spherical shell at a point outside the shell.
View SolutionState Gauss's theorem. Obtain an expression for elactric field at any point outside a charged spherical hollow conductor (shell).
View SolutionState Gauss's theorem. Obtain an expression for elactric field at any point outside a charged spherical hollow conductor (shell).
View SolutionState Gauss's theorem in electrostatics. Apply this theorem to derive an expression for electric field intensity at a point outside a uniformly charged thin spherical shell.
View SolutionState Gauss's theorem with the help of diagram, derive an expression for the electric field intensity due to uniformly charged thin spherical shell at a point outside
View SolutionState Gauss's theorem with the help of diagram, derive an expression for the electric field intensity due to uniformly charged thin spherical shell at a point inside
View SolutionState Gauss's theorem with the help of diagram, derive an expression for the electric field intensity due to uniformly charged thin spherical shell at a point on the surface of the spherical shell.
View SolutionDerive an expression for electric field due to a uniformly charged spherical shell. i) at a point outside the shell
View SolutionDerive the expression for electric field intensity due to a uniformly charged thin spherical shell at a point outside the shell
View Solution

