State Gauss' theorem in electrostatics. Using it, derive an expression for the electric charged thin spherical shell at a point insideSolution in Punjabi
Gauss.s Theorem : It states that total electric flux through a closed surface enclosing a charge is equal to 1ε0 times the magnitude of charge enclosed. Mathematical form of Gauss.s Las :
Electric flux =ϕ=∮→E.−→dSqε0
Electric field intensity due to an infinite plane thin sheet of charge :
Consider a thin, infinite plane sheet of charge.
Let σ = Surface charge density on both sides
Consider a point P at a distance r from the sheet.
Draw a cylindrical Gaussian surface of cross - section S through the point P with lenght r on each side of the cap.
Electric field E is perpendicular to its end circular Cpas I and II.
Charge enclosed by the Gaussian surface = q=σS
Using Gauss.s theorem
∮→E.−→dS=qε0=σSε0
Gaussian surface is divided into three parts, I II and III
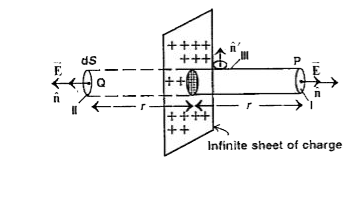
∴ Eqn. (i) becomes ∮I→E.−→dS+II–––∮→E.−→dS+∮III→E.−→dS=σSε0
Angle between →Eand−→dS is 90∘ for the curved III. In this case ∮III→E.−→dS=E.dScos90∘=0
Hence eqn. (ii) becomes ∮I→E.−→dS=undereset(II)∮→E.−→dS=σSε0
Since angle between →Eand−→dS for surface I and II is zero, so
∮I→E.dScos0∘+∮IIE.dScos0∘=σSε0or∮IE.dS+∮IIEdS=σSε0
Since electric field intensity E is Constant at very point of the Gaussian surface so
∴E∮IdS+E∮IIdS=σAε0orES+ES=σSε0[∴∮dS=S=Area of end cap]
or 2ES=σε0
or E=σ2ε0
If the plane sheet has a finite thickness : then charges on both sides of the sheet are to be considered. Thus equation (i) is written as ∫→E.−→dS=2σSε0
Then above eqn. becomes 2ES = 2simgmaε0 i.e., E=σε0 [theregore∫→E.−→dS=2ES]
Topper's Solved these Questions
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - GAUSS'S THEOREMEXERCISE - MOST EXPECTED NUMERICALS4videos
GAUSS'S THEOREM
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - GAUSS'S THEOREMEXERCISE - SHORT ANSWER TYPE QUESTIONS8videos
GAUSS'S THEOREM
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - FORCE ON A CURRENTEXERCISE - NUMERICAL PROBLEMS10videos
FORCE ON A CURRENT
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - HUYGENS' PRINCIPLEEXERCISE - LONG ANSWER TYPE QUESTIONS11videos
HUYGENS' PRINCIPLE
Similar Questions
A box encloses an electric dipole of 3μCand−3C, if the dipole length is 6 cm, then find total electric flux associated with box.
04:20View SolutionWhat is the use of Gaussian surface in electrostatics ?
05:56View SolutionA currentof 5.0 A is flowing in eah of the two parallel conductors of infinite length separated by certain distance apart in vacuum in the same directions. Each conductor expereinces a force of 2×10−4Nm−1 due to the other. Find the separation between the two conductors.
07:37View SolutionState Huygen's principle of propagation of light and prove the laws (Snell's law) of refraction on its basis.
03:31View SolutionUsing Gauss' law deduce the expression for the electric field due to a uniformly charge spherical conducting shell of radius R at a point (ii) inside the shell.
04:34View Solutionस्थिर वैधुतिकी में गाउस का प्रमेय लिखिए। इसका उपयोग करते हुए एकसमान आवेशित किसी पतले गोलीय खोल के बहार स्थित किसी बिंदु पर विधुत क्षेत्र हेतु व्यंजक विउत्पन्न व्युत्पन्न कीजिए।
05:18View Solutionगाउस की प्रमेय का उपयोग करके किसी बिन्दु पर विद्युत क्षेत्र की तीव्रता ज्ञात कीजिए-
समान रूप से आवेशित गोलीय कोश के कारण04:23View SolutionUsing Gauss's law in electrostatics, obtain an expression for electric field due to a uniformly charged thin spherical shell at a point
(i) Outside the shell and
(ii) Inside the shell05:28View SolutionDerive an expression for electric intensity E due to a uniformly charged thin spherical shell at a point outside the shell.
03:55View SolutionState Gauss's theorem. Obtain an expression for elactric field at any point outside a charged spherical hollow conductor (shell).
10:17View SolutionState Gauss's theorem in electrostatics. Apply this theorem to derive an expression for electric field intensity at a point outside a uniformly charged thin spherical shell.
View SolutionState Gauss's theorem with the help of diagram, derive an expression for the electric field intensity due to uniformly charged thin spherical shell at a point outside
08:05View SolutionState Gauss's theorem with the help of diagram, derive an expression for the electric field intensity due to uniformly charged thin spherical shell at a point inside
06:13View SolutionState Gauss's theorem with the help of diagram, derive an expression for the electric field intensity due to uniformly charged thin spherical shell at a point on the surface of the spherical shell.
07:26View SolutionState Gauss theorem in electrostatics. Derive the expression for electric field at a point due to an infinitely long straight charged conductor.
05:28View SolutionDerive the expression for electric field intensity due to a uniformly charged thin spherical shell at a point outside the shell
View Solution