In a , the sides PQ and PR and are produced to S and T respectively. Bisectors of meet at the point O. If , then what is the value of ?
The correct Answer is:C
To find the value of angle QOR in triangle PQR, we will follow these steps:
1. Identify Given Information:
- We have triangle PQR with angle P = 66°.
- The sides PQ and PR are extended to points S and T respectively.
- The angle bisectors of angles SQR and QRT meet at point O.
2. Use the Exterior Angle Theorem:
- According to the exterior angle theorem, the exterior angle (angle SQR) is equal to the sum of the two opposite interior angles (angle P and angle Q).
- Therefore, angle SQR = angle P + angle Q = 66° + β (where β is angle Q).
3. Similarly for Angle QRT:
- By the same theorem, angle QRT = angle P + angle R = 66° + α (where α is angle R).
4. Apply the Angle Sum Property in Triangle PQR:
- The sum of angles in triangle PQR is 180°.
- Thus, we have:
66°+α+β=180°
- Rearranging gives us:
α+β=180°−66°=114°
5. Determine Angles at Point O:
- Since O is the intersection of the angle bisectors, we can express the angles at O:
- Angle OQR = Angle OQS = (66° + β) / 2
- Angle ORQ = Angle ORT = (66° + α) / 2
6. Sum of Angles in Triangle RQO:
- In triangle RQO, we apply the angle sum property again:
AngleOQR+AngleORQ+AngleQOR=180°
- Substituting the expressions we found:
(33°+β2)+(33°+α2)+AngleQOR=180°
7. Combine and Simplify:
- This simplifies to:
66°+α+β2+AngleQOR=180°
- We know from step 4 that α + β = 114°, so:
66°+114°2+AngleQOR=180°
- This further simplifies to:
66°+57°+AngleQOR=180°
- Therefore:
AngleQOR=180°−123°=57°
Final Answer:
The value of angle QOR is 57°.
---
- We have triangle PQR with angle P = 66°.
- The sides PQ and PR are extended to points S and T respectively.
- The angle bisectors of angles SQR and QRT meet at point O.
- According to the exterior angle theorem, the exterior angle (angle SQR) is equal to the sum of the two opposite interior angles (angle P and angle Q).
- Therefore, angle SQR = angle P + angle Q = 66° + β (where β is angle Q).
- By the same theorem, angle QRT = angle P + angle R = 66° + α (where α is angle R).
- The sum of angles in triangle PQR is 180°.
- Thus, we have:
66°+α+β=180°
- Rearranging gives us:
α+β=180°−66°=114°
- Since O is the intersection of the angle bisectors, we can express the angles at O:
- Angle OQR = Angle OQS = (66° + β) / 2
- Angle ORQ = Angle ORT = (66° + α) / 2
- In triangle RQO, we apply the angle sum property again:
AngleOQR+AngleORQ+AngleQOR=180°
- Substituting the expressions we found:
(33°+β2)+(33°+α2)+AngleQOR=180°
- This simplifies to:
66°+α+β2+AngleQOR=180°
- We know from step 4 that α + β = 114°, so:
66°+114°2+AngleQOR=180°
- This further simplifies to:
66°+57°+AngleQOR=180°
- Therefore:
AngleQOR=180°−123°=57°
The value of angle QOR is 57°.
Topper's Solved these Questions
- TRIANGLESBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - Self Assessment Sheet - 18
10 Videos
- TRIANGLESBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - Self Assessment Sheet - 18
10 Videos
- TIME AND WORK BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - TIME AND WORK EXERCISE - Self Assessment Sheet - 13
15 Videos
- VOLUME AND SURFACE AREA OF A CUBE AND A CUBOIDBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - VOLUME AND SURFACE AREA OF A CUBE AND A CUBOIDEXERCISE - UNIT TEST - 5
20 Videos
Similar Questions
The sides PQ and PR of △PQR are produced to points S and T, respectively. The bisectors of ∠SQR and ∠TRQ meet at U. If ∠QUR=79∘ , then the measure of ∠P is:
त्रिभुज PQR की भुजाओ PQ और QR को क्रमशः S और T तक बढ़ाया जाता है| ∠SQR और ∠TRQ के समद्विभाजक U पर मिलते हैं| यदि ∠QUR=79∘ है, तो कोण P का मान ज्ञात करें |
View SolutionThe sides PQ and PR od △PQR are produced to point S and T, respectively. The bisector of ∠SQR and ∠TRQ, meet at U. If ∠QUR=59∘, then the measure of ∠P is:
△PQR की भुजाएँ PQ और PR क्रमशः बिंदु S और T तक बढ़ाया जाता हैं।∠SQR और ∠TRQ के द्विभाजक, U पर मिलते हैं। यदि ∠QUR=59∘ है, तो ∠P का माप है :
View Solution
Knowledge Check
In triangle PQR, the sides PQ and PR are produced to A and B respectively. The bisectors of ∠AQR and ∠BRQ intersect at point O. If ∠QOR=50∘, what is the value (in degree) of ∠QPR?
A1) 50B2) 60C3) 80D4)100In triangle PQR, the sides PQ and PR are produced to A and B respectively. The bisectors of ∠AQRand ∠BRQ intersect at point O. If ∠QOR=50∘, what is the value (in degree) of ∠QPR?
A50B60C80D100The sides AB and AC of △ABC are produced to points D and E, respectiely. The bisectors of ∠CBD and ∠BCE meet at P. If ∠A=82∘, then the measure of ∠P is :
A54∘B60∘C36∘D49∘
The sides AB and AC of △ABC are produced to points D and E, respectively. The bisectors of ∠CBDand∠BCE meet at P. If ∠A=72∘, then the measure of ∠P is:
View SolutionIn a △ABC, ∠A=52∘. Its sides AB and AC are produced to the points D and E respectively. If the bisectors of the ∠CBD and ∠BCE meet at point O, then ∠BOC is equal to:
△ABC में ∠A=52∘ है। इनकी भुजाएं AB और AC क्रमशः D और E तक बढाई जाती है। अगर ∠CBD और ∠BCE समदूविभाजक बिंदु O पर मिलते हैं, तो ∠BOC बराबर हैः
View SolutionInternal bisectors of ∠Q and ∠R of traingle PQR intersect at O.If angle ROQ= 96 then the value of angle RPQ is
View SolutionIn figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of ∠PBCand∠QCB intersect at O. Then, ∠BOC is equal to
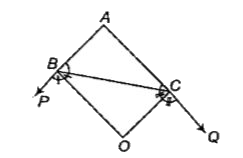
View SolutionΔABC ,angle B external angle C meets at P ∠A=80 then ∠BPC = ?
View Solution
