If ABCD is a square, X is the mid point of AB and Y is the mid point of BC, then which of the following is NOT correct?
The triangles ADX and BAY are congruent
∠DXA=∠AYB
∠ADX=∠BAY
DX is not perpendicular to AY
The correct Answer is:D
To solve the problem, we need to analyze the given square ABCD and the midpoints X and Y. We will then check the statements regarding the triangles formed.
1. Identify the Square and Midpoints:
- Let the vertices of the square ABCD be:
- A(0, 0)
- B(1, 0)
- C(1, 1)
- D(0, 1)
- The midpoint X of AB is:
- X = ((0 + 1)/2, (0 + 0)/2) = (0.5, 0)
- The midpoint Y of BC is:
- Y = ((1 + 1)/2, (0 + 1)/2) = (1, 0.5)
2. Identify the Triangles:
- We have two triangles to consider:
- Triangle AXY (with vertices A, X, Y)
- Triangle BXY (with vertices B, X, Y)
3. Check the Congruence of Triangles:
- For two triangles to be congruent, they must have:
- Three pairs of equal sides or
- Two pairs of equal sides and the included angle or
- Three pairs of equal angles.
- We will check the sides and angles of triangles AXY and BXY.
4. Calculate the Lengths of the Sides:
- Length of AX:
- AX = distance from A(0, 0) to X(0.5, 0) = 0.5
- Length of XY:
- XY = distance from X(0.5, 0) to Y(1, 0.5) = √((1 - 0.5)² + (0.5 - 0)²) = √(0.25 + 0.25) = √0.5
- Length of AY:
- AY = distance from A(0, 0) to Y(1, 0.5) = √((1 - 0)² + (0.5 - 0)²) = √(1 + 0.25) = √1.25
5. Check the Angles:
- Angle AXY and angle BXY can be calculated using the slopes of the lines:
- Slope of AX = (0 - 0)/(0.5 - 0) = 0
- Slope of AY = (0.5 - 0)/(1 - 0) = 0.5
- Since both triangles share the angle at X, we can compare the remaining angles.
6. Conclusion:
- After checking the sides and angles, we can conclude that the triangles AXY and BXY are not congruent.
- Therefore, the statement that claims they are congruent is NOT correct.
Final Answer:
The statement that triangle AXY is congruent to triangle BXY is NOT correct.
- Let the vertices of the square ABCD be:
- A(0, 0)
- B(1, 0)
- C(1, 1)
- D(0, 1)
- The midpoint X of AB is:
- X = ((0 + 1)/2, (0 + 0)/2) = (0.5, 0)
- The midpoint Y of BC is:
- Y = ((1 + 1)/2, (0 + 1)/2) = (1, 0.5)
- We have two triangles to consider:
- Triangle AXY (with vertices A, X, Y)
- Triangle BXY (with vertices B, X, Y)
- For two triangles to be congruent, they must have:
- Three pairs of equal sides or
- Two pairs of equal sides and the included angle or
- Three pairs of equal angles.
- We will check the sides and angles of triangles AXY and BXY.
- Length of AX:
- AX = distance from A(0, 0) to X(0.5, 0) = 0.5
- Length of XY:
- XY = distance from X(0.5, 0) to Y(1, 0.5) = √((1 - 0.5)² + (0.5 - 0)²) = √(0.25 + 0.25) = √0.5
- Length of AY:
- AY = distance from A(0, 0) to Y(1, 0.5) = √((1 - 0)² + (0.5 - 0)²) = √(1 + 0.25) = √1.25
- Angle AXY and angle BXY can be calculated using the slopes of the lines:
- Slope of AX = (0 - 0)/(0.5 - 0) = 0
- Slope of AY = (0.5 - 0)/(1 - 0) = 0.5
- Since both triangles share the angle at X, we can compare the remaining angles.
- After checking the sides and angles, we can conclude that the triangles AXY and BXY are not congruent.
- Therefore, the statement that claims they are congruent is NOT correct.
The statement that triangle AXY is congruent to triangle BXY is NOT correct.
Topper's Solved these Questions
- TRIANGLESBook:S CHAND IIT JEE FOUNDATIONChapter:TRIANGLESExercise:Self Assessment Sheet - 18
Explore 10 Videos
- TRIANGLESBook:S CHAND IIT JEE FOUNDATIONChapter:TRIANGLESExercise:Self Assessment Sheet - 18
Explore 10 Videos
- TIME AND WORK Book:S CHAND IIT JEE FOUNDATIONChapter:TIME AND WORK Exercise:Self Assessment Sheet - 13
Explore 15 Videos
- VOLUME AND SURFACE AREA OF A CUBE AND A CUBOIDBook:S CHAND IIT JEE FOUNDATIONChapter:VOLUME AND SURFACE AREA OF A CUBE AND A CUBOIDExercise:UNIT TEST - 5
Explore 20 Videos
Similar Questions
Knowledge Check
If C is the mid-point of AB and P is any point outside AB, then
APA + PB = PCBPA + PB + 2 PC = 0CPA + PB - 2PC = 0DPA + PB + PC = 0If C is the mid-point of AB and P is any point outside AB, then
APA+PB+PC=0BPA+PB+2PC=0CPA+PB=PCDPA+PB=2PCABCD is a square. M is the mid-point of AB and N is the mid-point of BC. DM and AN are joined and they meet at O, then which of the following is correct ?
AOA : OM = 1 : 2BAN = MDC∠ADM=∠ANBD∠AMD=∠BAN
in figure , M is the mid-point of AB and N is the mid-point of BC (1) if AB=BC , prove that AM=NC
View Solutionin figure , M is the mid-point of AB and N is the mid-point of BC (1) if AB=BC , prove that AM=NC
View SolutionLocus of mid point of AB is
View SolutionIn the following figure, PQRS is a square. M is the mid-point of PQ and AB⊥RM. Then, which of the following is false?
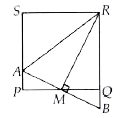
View SolutionFigure showns three vectors p,q and r where C is the mid - point of AB Then which of the following reation is correct ?

View Solution