In ΔABC medians BE and CF intersect at G. If the straight line AGD meets BC in D in such a way that GD = 1.5 cm, then the length of AD is :
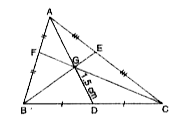
In Delta ABC medians BE and CF intersect at G. If the straight line AGD meets BC in D in such a way that GD = 1.5 cm, then the length of AD is :

A

2.5 cm

B

3 cm

C

4 cm

D

4.5 cm

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:D

Updated on:21/07/2023
|
Answer

Step by step video, text & image solution for In Delta ABC medians BE and CF intersect at G. If the straight line AGD meets BC in D in such a way that GD = 1.5 cm, then the length of AD is : by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.

Updated on:21/07/2023
Class 7MATHSTRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • In ΔABC, the median AD, BE and CF at G. then which of the following is correct?

    AAD+BE+CF>12(AB+BC+AC)
    B2(AD+BE+CF)>(AB+BC+AC)
    C3(AD+BE+CF)>4(AB+BC+AC)
    DAB+BC+AC>AD+BE+CF

  • O is the centroid of △ABC. The medians AD and BE intersect at right angles. If the lenghts of AD and BE are 9 cm and 12 cm respectively : then the length of AB (in cm) is

    A9.5
    B10
    C11
    D10.5

  • Three medians AD, BE and CF of ΔABC intersect at G. The area of ΔABC is 36 sq. cm. Then the area of ΔCGE is

    A12 sq. cm
    B6 sq. cm
    C9 sq. cm
    D18 sq. cm