The medians BE and CF of a △ABC intersect at G. Then choose the correct option.

A

ar(△GBC) = ar of quad.AFGE

B

ar(△GBC)=ar(△FCB)

C

ar(△GBC)=ar(/_\AFC)

D

ar(△BGC) = ar (BACG)

Video Solution
Doubtnut Promotions Banner
Text Solution
Generated By DoubtnutGPT

To solve the problem, we need to analyze the triangle ABC with medians BE and CF intersecting at point G. We will find the relationship between the areas of the triangles formed by these medians.

1. Draw Triangle ABC:
- Start by sketching triangle ABC. Mark points A, B, and C.

2. Identify the Medians:
- Draw median BE from vertex B to the midpoint E of side AC.
- Draw median CF from vertex C to the midpoint F of side AB.

3. Mark the Intersection Point:
- Label the intersection of medians BE and CF as point G.

4. Divide the Triangle into Areas:
- The medians divide triangle ABC into six smaller triangles: AGB, AGC, BGE, BGC, CFE, and CGF.
- Let's denote the areas of these triangles as follows:
- Area of triangle AGB = 1
- Area of triangle AGC = 2
- Area of triangle BGE = 3
- Area of triangle BGC = 4
- Area of triangle CFE = 5
- Area of triangle CGF = 6

5. Use the Properties of Medians:
- Since BE is a median, it divides triangle ABC into two equal areas:
- Area of triangle ABE = Area of triangle BCE.
- Similarly, CF is also a median, so it divides triangle ABC into two equal areas:
- Area of triangle ACF = Area of triangle BCF.

6. Set Up Area Equations:
- From the properties of medians, we can write:
- Area of triangle ABE = Area of triangle BCE = Area of triangle ACF = Area of triangle BCF.
- This means:
- Area of triangle BGC = Area of triangle BGE + Area of triangle GBC = 3 + x (where x is the area of triangle GBC).
- Area of triangle AGB + Area of triangle AGC = 1 + 2 = 3.
- Area of triangle AGB + Area of triangle BGC = 1 + (3 + x) = 4 + x.

7. Equate Areas:
- Since the total area of triangle ABC is constant, we can set up the equation:
- Area of triangle AGB + Area of triangle AGC + Area of triangle BGC = Area of triangle ABE + Area of triangle BGC.
- This simplifies to:
- 3 + x = 4 + x.

8. Solve for Areas:
- By solving the equation, we find that:
- Area of triangle GBC = Area of quadrilateral AFG.
- Thus, we conclude that the area of triangle GBC is equal to the area of quadrilateral AFG.

Conclusion:
The correct option is that the area of triangle GBC equals the area of quadrilateral AFG.

Updated on:18/9/2024
|
Class 11MATHSQUESTION BANK

Similar Questions

Knowledge Check

  • Choose the correct options.

    ACell division helps group of cells to undergo certain modification to form specialised organs.
    BCell differentiation helps in increasing the number of cells.
    CIn viviparous animals, development of zygote takes place inside the body.
    DAll of the above.

  • Choose the correct options:

    AFavourable conditions for formation of graphite are high pressure and low temperature from equilibrium diamond (d=3.5g/ml)⇔ graphite (d=2.3g/ml),Δ=−1.9kJ/mole
    BFor reaction N2O4(g)⇔2NO,(g), degree of dissociation (α) is √K4P+KP where P is equilibrium pressure.
    CFor reaction CI2(g)+3F2(g)⇔2CIF3(g),ΔH=−329kJ ,dissociation of CIF3(g) will be favoured by additon of inert gas at constant pressure.
    DReaction stops at equilibrium (microscopically).

  • Choose the correct option(s)

    A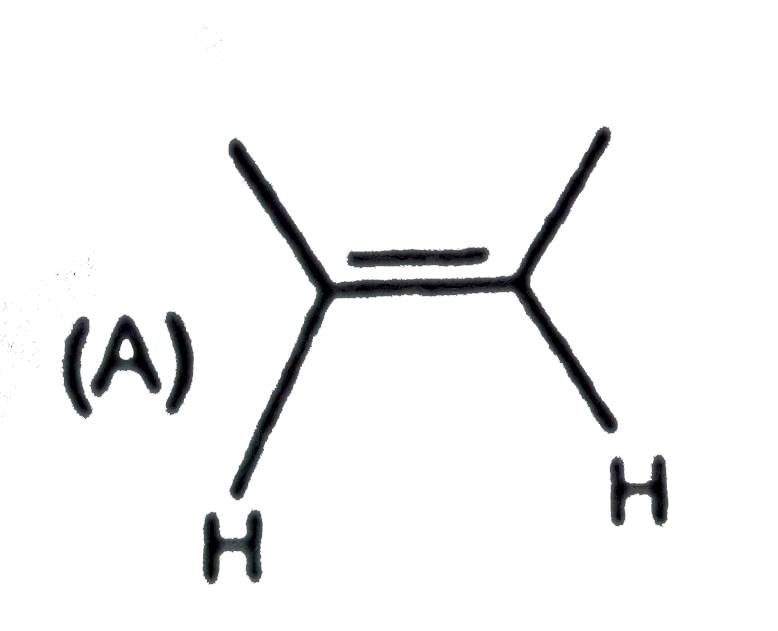ocr_image HOBr−−−→ Major products are enantiomers
    B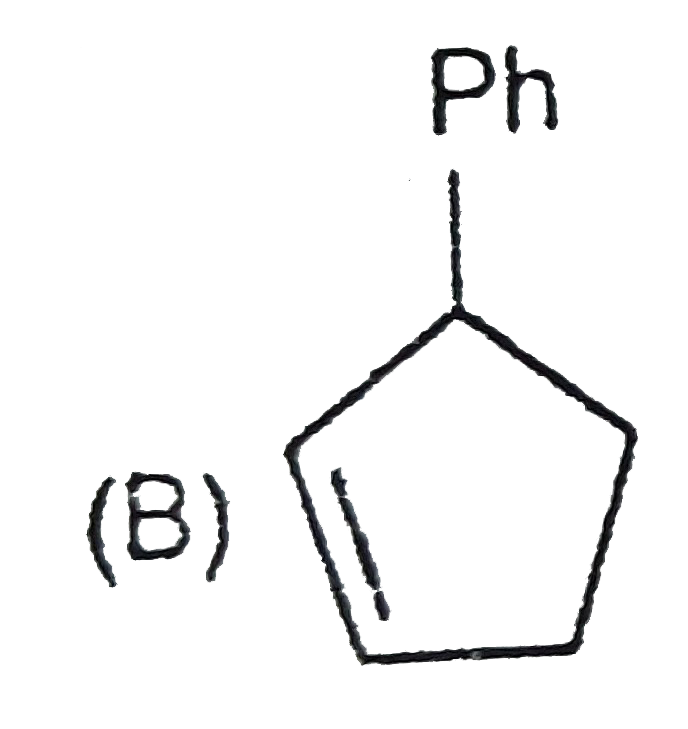ocr_image H3O⊕−−−→ Major products is optically active
    CCH2=CH2OsO4/NaHSO3−−−−−−−−−→ product is CH2∣OH−CH2∣OH
    D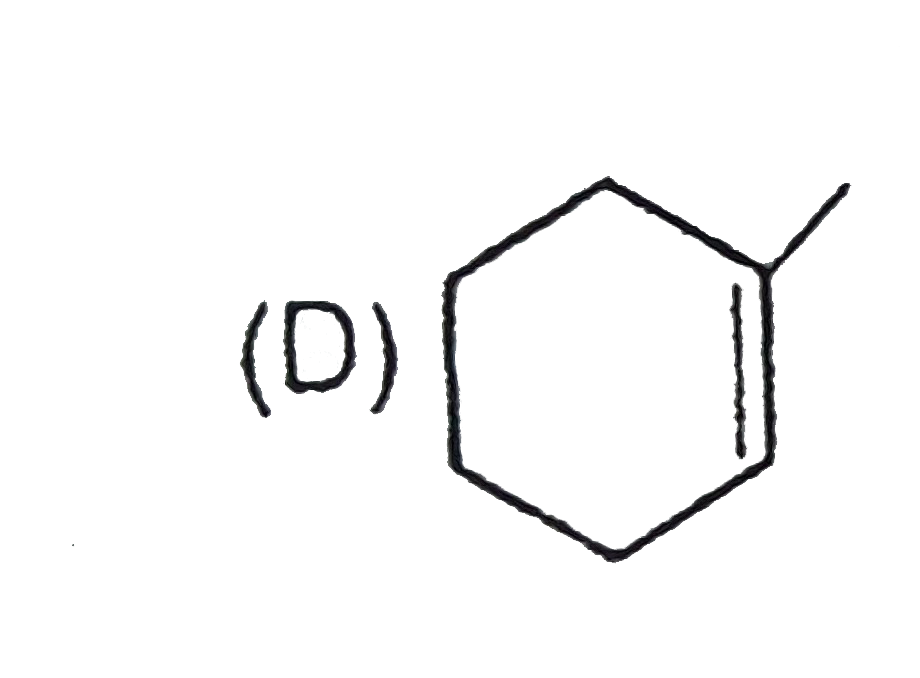ocr_image MCPBA−−−−→ products are diasteromers