In triangle PQR, the sides PQ and PR are produced to A and B respectively. The bisectors of ∠AQRand ∠BRQ intersect at point O. If ∠QOR=50∘, what is the value (in degree) of ∠QPR?
50
60
80
100
The correct Answer is:C
To solve the problem, we need to find the value of angle ∠QPR in triangle PQR given that the angle ∠QOR=50∘. We know that O is the intersection of the angle bisectors of ∠AQR and ∠BRQ.
1. Understand the Geometry:
- We have triangle PQR.
- The sides PQ and PR are extended to points A and B respectively.
- The angle bisectors of ∠AQR and ∠BRQ intersect at point O.
- We are given that ∠QOR=50∘.
2. Use the Property of the Excenter:
- The point O is the excenter of triangle PQR opposite to vertex P.
- The property of the excenter states that:
∠QOR=90∘−12∠QPR
3. Set Up the Equation:
- From the property mentioned, we can set up the equation:
50∘=90∘−12∠QPR
4. Rearrange the Equation:
- Rearranging the equation gives:
12∠QPR=90∘−50∘
12∠QPR=40∘
5. Solve for ∠QPR:
- Multiplying both sides by 2:
∠QPR=2×40∘=80∘
Final Answer:
Thus, the value of ∠QPR is 80∘.
---
- We have triangle PQR.
- The sides PQ and PR are extended to points A and B respectively.
- The angle bisectors of ∠AQR and ∠BRQ intersect at point O.
- We are given that ∠QOR=50∘.
- The point O is the excenter of triangle PQR opposite to vertex P.
- The property of the excenter states that:
∠QOR=90∘−12∠QPR
- From the property mentioned, we can set up the equation:
50∘=90∘−12∠QPR
- Rearranging the equation gives:
12∠QPR=90∘−50∘
12∠QPR=40∘
- Multiplying both sides by 2:
∠QPR=2×40∘=80∘
Thus, the value of ∠QPR is 80∘.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-IV)
Explore 35 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-V)
Explore 30 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-II)
Explore 25 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
In triangle PQR, the internal bisector of ∠Q and ∠R meets at 0. If ∠QPR=70∘, then what is the value (in degrees) of ∠QOR?
View SolutionThe sides PQ and PR od △PQR are produced to point S and T, respectively. The bisector of ∠SQR and ∠TRQ, meet at U. If ∠QUR=59∘, then the measure of ∠P is:
△PQR की भुजाएँ PQ और PR क्रमशः बिंदु S और T तक बढ़ाया जाता हैं।∠SQR और ∠TRQ के द्विभाजक, U पर मिलते हैं। यदि ∠QUR=59∘ है, तो ∠P का माप है :
View Solution
Knowledge Check
In triangle PQR, the sides PQ and PR are produced to A and B respectively. The bisectors of ∠AQR and ∠BRQ intersect at point O. If ∠QOR=50∘, what is the value (in degree) of ∠QPR?
A1) 50B2) 60C3) 80D4)100In triangle PQR, the internal bisector of ∠Q and ∠R meets at 0. If ∠QPR=70∘, then what is the value (in degrees) of ∠QOR?
A45B125C115D110In a ΔPQR, the sides PQ and PR and are produced to S and T respectively. Bisectors of ∠SQRand∠QRT meet at the point O. If ∠P=66∘, then what is the value of ∠QOR?
A47∘B50∘C57∘D67∘
If O is the circum-centre in ΔPQRand∠QOR=40∘, then what is the value (in degrees) of ∠QPR?
View SolutionIn figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of <PBC and <QCB intersect at O. Tnen. <BOC is equal to
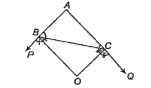
View SolutionPQRS is a cyclic quadrilateral. PR and QS intersect at T. If ∠SPR=40∘and∠PQS=80∘, then what is the value (in degrees) of ∠PSR?
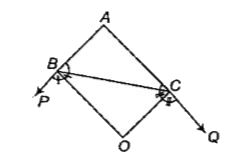
View SolutionIn figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of ∠PBCand∠QCB intersect at O. Then, ∠BOC is equal to
View SolutionIn the given figure. 0 is centre of the circle. Circle has 3 tangents. If QPR = 45∘, then what is the value (in degrees) of ∠QOR?

View Solution
