If O is the circum-centre in ΔPQRand∠QOR=40∘, then what is the value (in degrees) of ∠QPR?
40
60
80
20
The correct Answer is:D
To find the value of angle ∠QPR in triangle ΔPQR given that O is the circumcenter and ∠QOR=40∘, we can follow these steps:
1. Understanding the Circumcenter:
- The circumcenter O of a triangle is the point where the perpendicular bisectors of the sides intersect. It is also the center of the circumcircle, which means all vertices of the triangle lie on this circle.
2. Identify the Given Angle:
- We are given that ∠QOR=40∘.
3. Using the Inscribed Angle Theorem:
- According to the inscribed angle theorem, the angle subtended at the center of the circle (in this case, ∠QOR) is twice the angle subtended at any point on the circumference (in this case, ∠QPR).
- Therefore, we can express this relationship mathematically as:
∠QPR=12∠QOR
4. Substituting the Known Value:
- Now, substituting the value of ∠QOR:
∠QPR=12×40∘=20∘
5. Final Answer:
- Thus, the value of ∠QPR is 20∘.
Summary:
The value of ∠QPR is 20∘.
- The circumcenter O of a triangle is the point where the perpendicular bisectors of the sides intersect. It is also the center of the circumcircle, which means all vertices of the triangle lie on this circle.
- We are given that ∠QOR=40∘.
- According to the inscribed angle theorem, the angle subtended at the center of the circle (in this case, ∠QOR) is twice the angle subtended at any point on the circumference (in this case, ∠QPR).
- Therefore, we can express this relationship mathematically as:
∠QPR=12∠QOR
- Now, substituting the value of ∠QOR:
∠QPR=12×40∘=20∘
- Thus, the value of ∠QPR is 20∘.
The value of ∠QPR is 20∘.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:TRY YOURSELF
Explore 25 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIII)
Explore 70 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
Knowledge Check
Triangle PQR is inscribed in a circle such that P Q and R lie on the circumference. If PQ is the diameter of the circle and ∠PQR=40∘, then what is the value (in degree) of QPR?
A40B45C50D55If P is the circum-center in ΔABC, ∠BPC=30∘, then what is the value (in degrees) of ∠BAC?
A30B60C75D15Two tangents are drawn from a point P to a circle at Q and R. If O is the centre of the circle and ∠QOP=40∘, then what is the value (in degrees) of ∠QPR?
A60B80C90D100
In the following figure, O is the centre of the circle and ∠PRQ=50∘. What is the value (in degrees) of ∠PTQ?
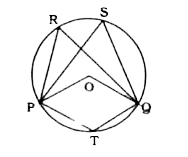
View SolutionIn the given figure. 0 is centre of the circle. Circle has 3 tangents. If QPR = 45∘, then what is the value (in degrees) of ∠QOR?

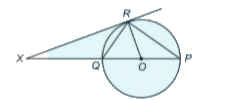
View SolutionXR is a tangent to the circle. O is the centre of the circle. If ∠XRP=120∘, then what is the value (in degrees) of ∠QOR?
View SolutionO is the incentre of ΔPQRand∠QPR=50∘, then the measure of ∠QOR is :
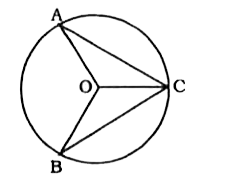
View SolutionIn the given figure, O is the centre of the circle, ∠CAO = 35∘ and ∠CBO= 45∘. What is the value (In degrees) of ∠AOB?
View Solution