In triangle PQR, the sides PQ and PR are produced to A and B respectively. The bisectors of ∠AQR and ∠BRQ intersect at point O. If ∠QOR=50∘, what is the value (in degree) of ∠QPR?
1) 50
2) 60
3) 80
4)100
The correct Answer is:C
To solve the problem, we need to find the value of angle QPR in triangle PQR given that angle QOR is 50 degrees. We will use the properties of angle bisectors and the relationships between angles in a triangle.
Step 1: Understand the Geometry
We have triangle PQR, and the sides PQ and PR are extended to points A and B respectively. The angle bisectors of angles AQR and BRQ intersect at point O. We are given that angle QOR = 50 degrees.
Step 2: Apply the Angle Bisector Theorem
From the properties of angle bisectors, we know that:
- The angle formed at point O by the bisectors of angles AQR and BRQ can be expressed in terms of angle QPR.
- Specifically, if we denote angle QPR as angle P, then the relationship is given by:
∠QOR=90∘−∠P2
Step 3: Substitute the Given Value
We know that angle QOR = 50 degrees. Thus, we can set up the equation:
50∘=90∘−∠P2
Step 4: Solve for Angle P
Rearranging the equation to isolate angle P:
∠P2=90∘−50∘
∠P2=40∘
Now, multiply both sides by 2 to find angle P:
∠P=80∘
Conclusion
Thus, the value of angle QPR is:
∠QPR=80∘
We have triangle PQR, and the sides PQ and PR are extended to points A and B respectively. The angle bisectors of angles AQR and BRQ intersect at point O. We are given that angle QOR = 50 degrees.
From the properties of angle bisectors, we know that:
- The angle formed at point O by the bisectors of angles AQR and BRQ can be expressed in terms of angle QPR.
- Specifically, if we denote angle QPR as angle P, then the relationship is given by:
∠QOR=90∘−∠P2
We know that angle QOR = 50 degrees. Thus, we can set up the equation:
50∘=90∘−∠P2
Rearranging the equation to isolate angle P:
∠P2=90∘−50∘
∠P2=40∘
Now, multiply both sides by 2 to find angle P:
∠P=80∘
Thus, the value of angle QPR is:
∠QPR=80∘
Similar Questions
Knowledge Check
In triangle PQR, the sides PQ and PR are produced to A and B respectively. The bisectors of ∠AQRand ∠BRQ intersect at point O. If ∠QOR=50∘, what is the value (in degree) of ∠QPR?
A50B60C80D100In a ΔPQR, the sides PQ and PR and are produced to S and T respectively. Bisectors of ∠SQRand∠QRT meet at the point O. If ∠P=66∘, then what is the value of ∠QOR?
A47∘B50∘C57∘D67∘In figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of ∠PBCand∠QCB intersect at O. Then, ∠BOC is equal to
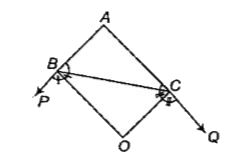 A90∘−12∠BACB12(∠PBC+∠QCB)C90∘+12∠BACDNone of the above
A90∘−12∠BACB12(∠PBC+∠QCB)C90∘+12∠BACDNone of the above
The sides PQ and PR od △PQR are produced to point S and T, respectively. The bisector of ∠SQR and ∠TRQ, meet at U. If ∠QUR=59∘, then the measure of ∠P is:
△PQR की भुजाएँ PQ और PR क्रमशः बिंदु S और T तक बढ़ाया जाता हैं।∠SQR और ∠TRQ के द्विभाजक, U पर मिलते हैं। यदि ∠QUR=59∘ है, तो ∠P का माप है :
View SolutionThe sides PQ and PR of △PQR are produced to points S and T, respectively. The bisectors of ∠SQR and ∠TRQ meet at U. If ∠QUR=79∘ , then the measure of ∠P is:
त्रिभुज PQR की भुजाओ PQ और QR को क्रमशः S और T तक बढ़ाया जाता है| ∠SQR और ∠TRQ के समद्विभाजक U पर मिलते हैं| यदि ∠QUR=79∘ है, तो कोण P का मान ज्ञात करें |
View SolutionIn a triangle ABC, the sides AB, AC are produced and the bisectors of exterior angles of ∠ABCand∠ACB intersect at D. If ∠BAC=50∘, then ∠BDC is equal to
View SolutionIn △ABC ,∠A=72∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=72∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के समद्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान ज्ञात करें |
View SolutionIn figure, sides AB and AC of a ΔABC are produced to P and Q, respectively. The bisectors of <PBC and <QCB intersect at O. Tnen. <BOC is equal to
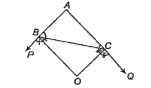
View Solution
