Consider the inequation x2+x+a−9<0
The values of the real parameter a so that the given inequations has at least one negative solution.Solution in Bengali
(−∞,9)
(374,∞)
(−∞,374)
none of these
The correct Answer is:3
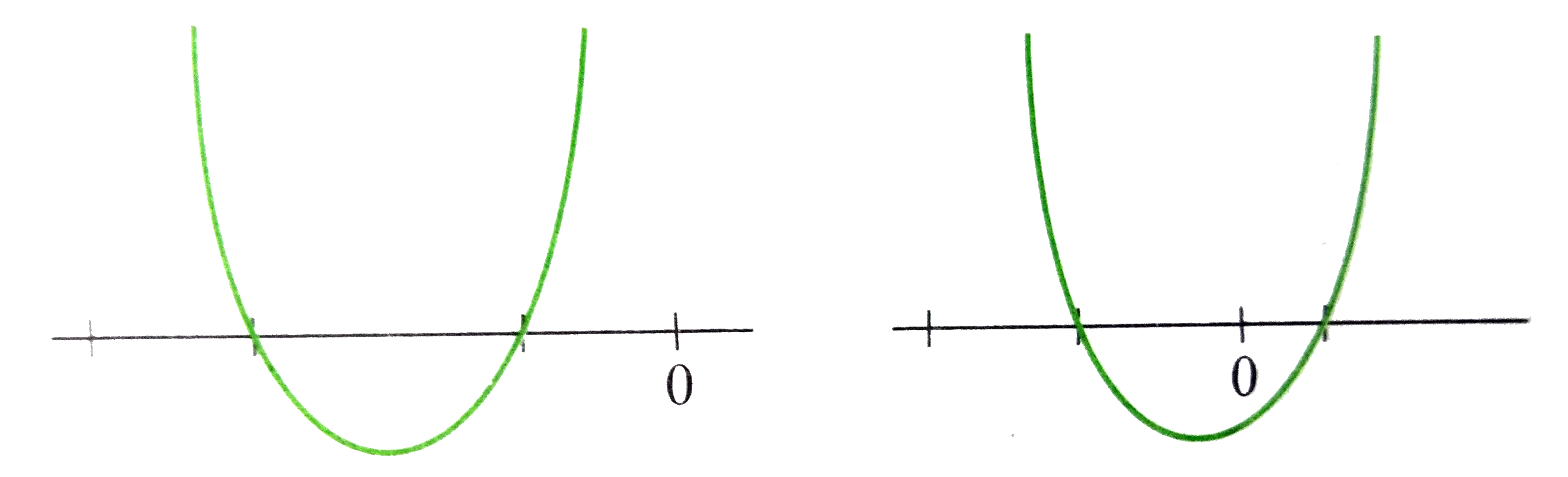
If x2+x+a−9<0 has at least one negative solution, then either both the roots of equations x2+x+a−9=0 are non-posititve or 0 lies between the roots.
For case I, sum of roots is a−9>0
⇒a>9and
D>0
⇒1−4(a−9)>0⇒a<374
Hence, 9≤a≤37/4.
For case II, f(0)>0
⇒a<9⇒a∈(−∞,374)
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - MATRIX MATCH TYPE6videos
THEORY OF EQUATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - NUMERICAL VALUE TYPE43videos
THEORY OF EQUATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer Type38videos
THEORY OF EQUATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)1videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions291videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
Match the following for the equation x2+a|x|+1=0 where, a is a parameter.
View SolutionIf x=2+22/3+21/3 , then the value of x3−6x2+6x is
01:23View SolutionIf c≠0 and the equation p2x=ax+c+bx−c has two equal roots, then p can be
02:27View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
00:58View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
02:50View SolutionConsider the inequality, 9x−a.3x−a+3≤0, where 'a' is a real parameter.
(a) Find the value of 'a' for which the inequality has at least one negative solution.
(b) Find the values of 'a' for which the inequality has at least one positive solution.
(c) Find the vlaues of 'a' for which the inequality has at least one real solution.03:10View SolutionConsider the inequation x2+x+a−9<0
The values of the real parameter a so that the given inequaiton has at least one positive solution:03:51View SolutionConsider the inequation x2+x+a−9<0
The values of the real parameter a so that the given inequations has at least one negative solution.02:47View SolutionConsider the inequation x2+x+a−9<0
The value of the parameter a so that the given inequaiton is ture ∀x∈(−1,3)02:13View SolutionConsider the inequation 9x−a3x−a+3≤0, where a is real parameter.
The given inequality has at least one negative soluiton for a∈02:50View SolutionConsider the inequation 9x−a3x−a+3≤0, where a is real parameter.
The given inequality has at least one real solutions for a∈.02:12View SolutionConsider the inequality 9x−a.3x−a+3≤0 where 'a' is a real parameter.
The given inequality has at least one negative solution for 'a' lying in-02:57View SolutionFind the graph of linear inequation in xy plane 2y+7≤0
02:03View SolutionFind the graph of linear inequation in xy plane 4x+8>0
09:18View SolutionConsider the inequation 9x−a3x−a+3≤0, where a is real parameter.
The given inequality has at least one negative solution for a∈ (a) (−∞,2) (b) (3,∞) (c) (−2,∞) (d) (2,3)03:50View SolutionConsider the inequation x2+x+a−9<0
The values of the real parameter a so that the given inequaiton has at least one positive solution:03:19View Solution