Consider the inequation x2+x+a−9<0
The values of the real parameter a so that the given inequaiton has at least one positive solution:
(−∞,37/4)
(−∞,∞)
(3,∞)
(−∞,9)
The correct Answer is:4
Let f(x)=x2+x+a−9
x2+x+a−9<0 has at least one positve solution, the either both the roots of equation x2+x+a−9=0 are non-negative or 0 lies betweens the roots.
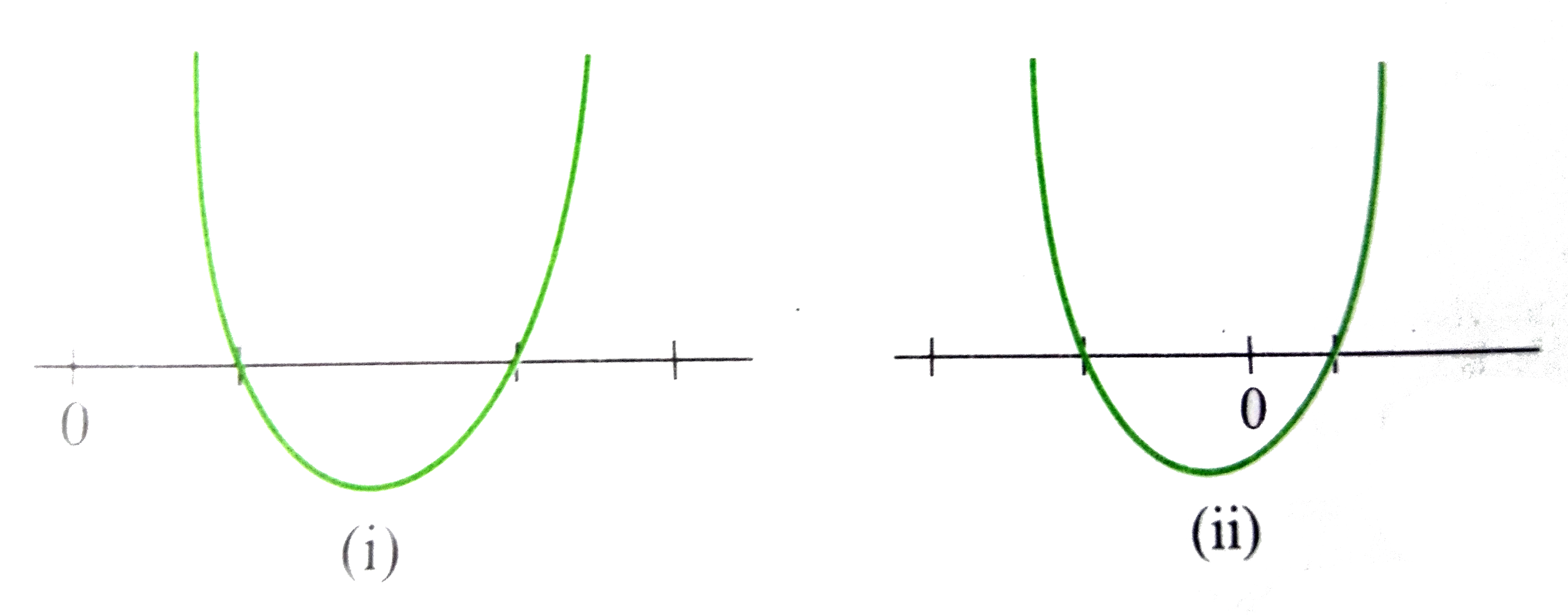
Now sum of roots =−(1), hence, case I is not possible . For Case II, f(0)<0⇒a−9<0ora<9
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - MATRIX MATCH TYPE
6 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - NUMERICAL VALUE TYPE
43 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer Type
38 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
Similar Questions
Consider the inequation x2+x+a−9<0
The values of the real parameter a so that the given inequations has at least one negative solution.
View SolutionConsider the inequation x2+x+a−9<0
The value of the parameter a so that the given inequaiton is ture ∀x∈(−1,3)
View SolutionConsider the inequation 9x−a3x−a+3≤0, where a is real parameter.
The given inequality has at least one negative solution for a∈ (a) (−∞,2) (b) (3,∞) (c) (−2,∞) (d) (2,3)
View SolutionFind the range of values of 'a' so that the equation x2−(a−5)x+(a−154)=0 has at least one positive root
View SolutionFind the possible values of 'a' such that the inequality 3−x2>|x−a| has atleast one negative solution
View SolutionFind all the values of the parameter 'a' for which the inequality 4x−a2x−a+3≤0 is satisfied by at least one real x.
View SolutionConsider the equation ∣∣x2−2x−3∣∣=m,m∈R.
If the given equation has two solutions, then:
View SolutionFind the number of integral value of n so that sinx(sinx+cosx)=n has at least one solution.
View SolutionLet f(x)=x2+3x+ax2+x+1 where f:R→R. Find the value of parameter a' so that the given function is one-one
View SolutionIf the equation ax2+bx+c=0 has two positive and real roots, then prove that the equation ax2+(b+6a)x+(c+3b)=0 has at least one positive real root.
View Solution
