Consider the inequality 9x−a⋅3x−a+3≤0, where a is a real parameter.
The given inequality has at least one positive solution for a∈
(−∞,3)
[2,∞)
(3,∞)
[−2,∞)
The correct Answer is:2
Given that 9x−a3x−a+3≤0
Let t=3x. Then,
t2−at−a+3≤0
or t3+3≤a(t+1) (1)
where t∈R+,∀x∈R
Let f1(t)=t2+3 and
f2(t)=a(t+1).
In this case both graphs should meet at least once is t∈(0,∞). For a= 2 both the curves touch , hence the required range is a∈[2,∞)
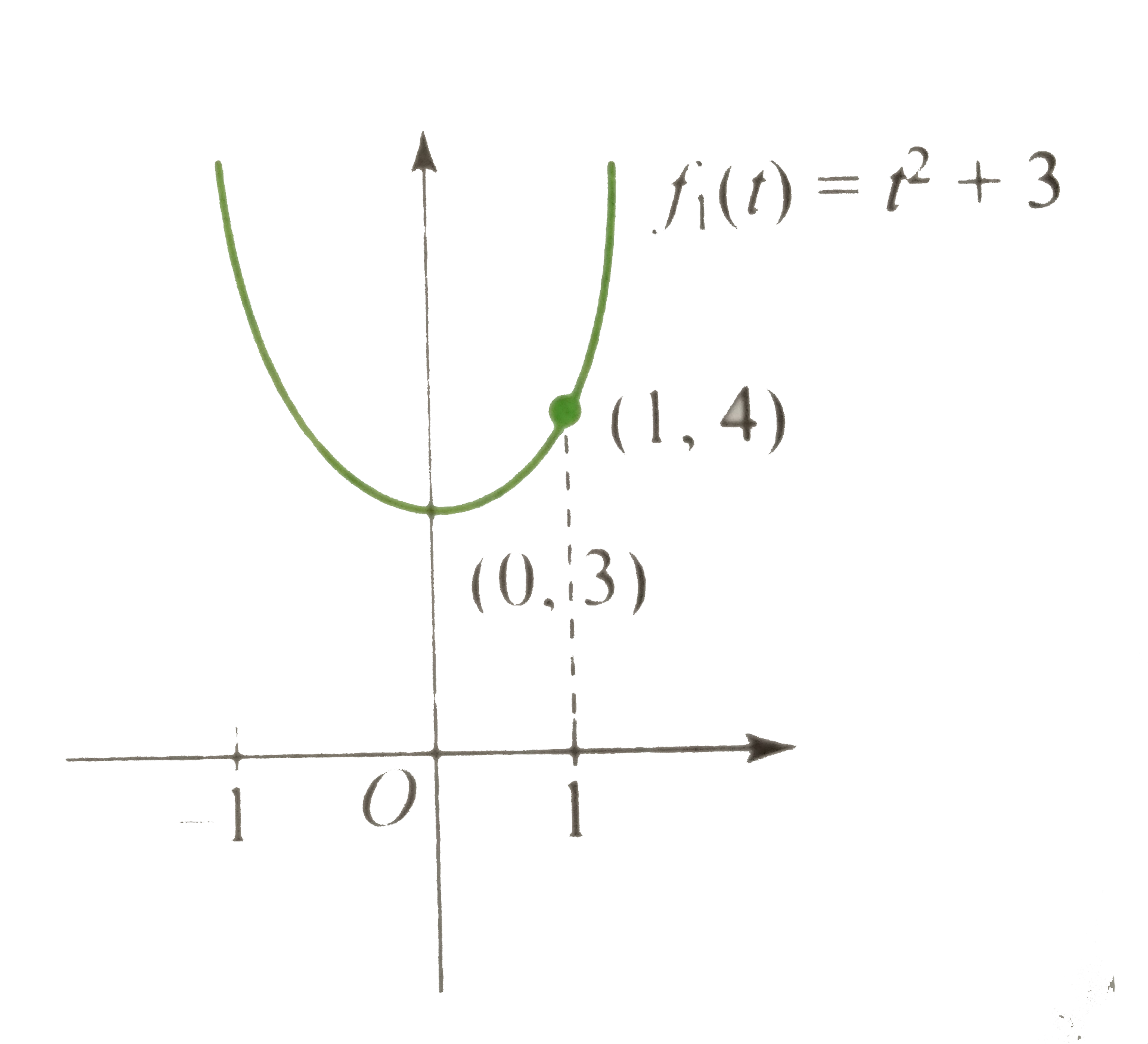
Topper's Solved these Questions
- THEORY OF EQUATIONSBook:CENGAGE ENGLISHChapter:THEORY OF EQUATIONSExercise:MATRIX MATCH TYPE
Explore 6 Videos
- THEORY OF EQUATIONSBook:CENGAGE ENGLISHChapter:THEORY OF EQUATIONSExercise:NUMERICAL VALUE TYPE
Explore 43 Videos
- THEORY OF EQUATIONSBook:CENGAGE ENGLISHChapter:THEORY OF EQUATIONSExercise:Multiple Correct Answer Type
Explore 38 Videos
- STRAIGHT LINESBook:CENGAGE ENGLISHChapter:STRAIGHT LINESExercise:ARCHIVES (NUMERICAL VALUE TYPE)
Explore 1 Video
- THREE DIMENSIONAL GEOMETRYBook:CENGAGE ENGLISHChapter:THREE DIMENSIONAL GEOMETRYExercise:All Questions
Explore 294 Videos
Similar Questions
Consider the inequation 9x−a3x−a+3≤0, where a is real parameter.
The given inequality has at least one negative solution for a∈ (a) (−∞,2) (b) (3,∞) (c) (−2,∞) (d) (2,3)
View SolutionConsider the inequation x2+x+a−9<0
The values of the real parameter a so that the given inequaiton has at least one positive solution:
View Solution
Knowledge Check
Consider the inequality y≥ax2+bx+c, where a , b and c are all positive . Which of the following regions could be the solution set of the inequality ?
A B
B C
C D
D
Consider the inequation x2+x+a−9<0
The values of the real parameter a so that the given inequations has at least one negative solution.
View SolutionConsider the inequation x2+x+a−9<0
The value of the parameter a so that the given inequaiton is ture ∀x∈(−1,3)
View SolutionSolve the inequation 2x−3<0
View SolutionSolve the inequation 3x+2>(19)1/x.
View SolutionSolve the inequation : −3≤4−7x2≤18
View SolutionFind the possible values of 'a' such that the inequality 3−x2>|x−a| has atleast one negative solution
View SolutionSolve the inequation 2≤|x−3|≤4
View Solution