If (x+2) is a common factor of (px2+qx+r) and (qx2+px+r) then (a) p=q or p+q+r=0 (b)p=r or p+q+r=0 (c) q=r or p+q+r=0 (d)p=q=−12rSolution in Bengali
|d|≤|D|
|d|≥|D|
|d|=|D|
None of these
The correct Answer is:1
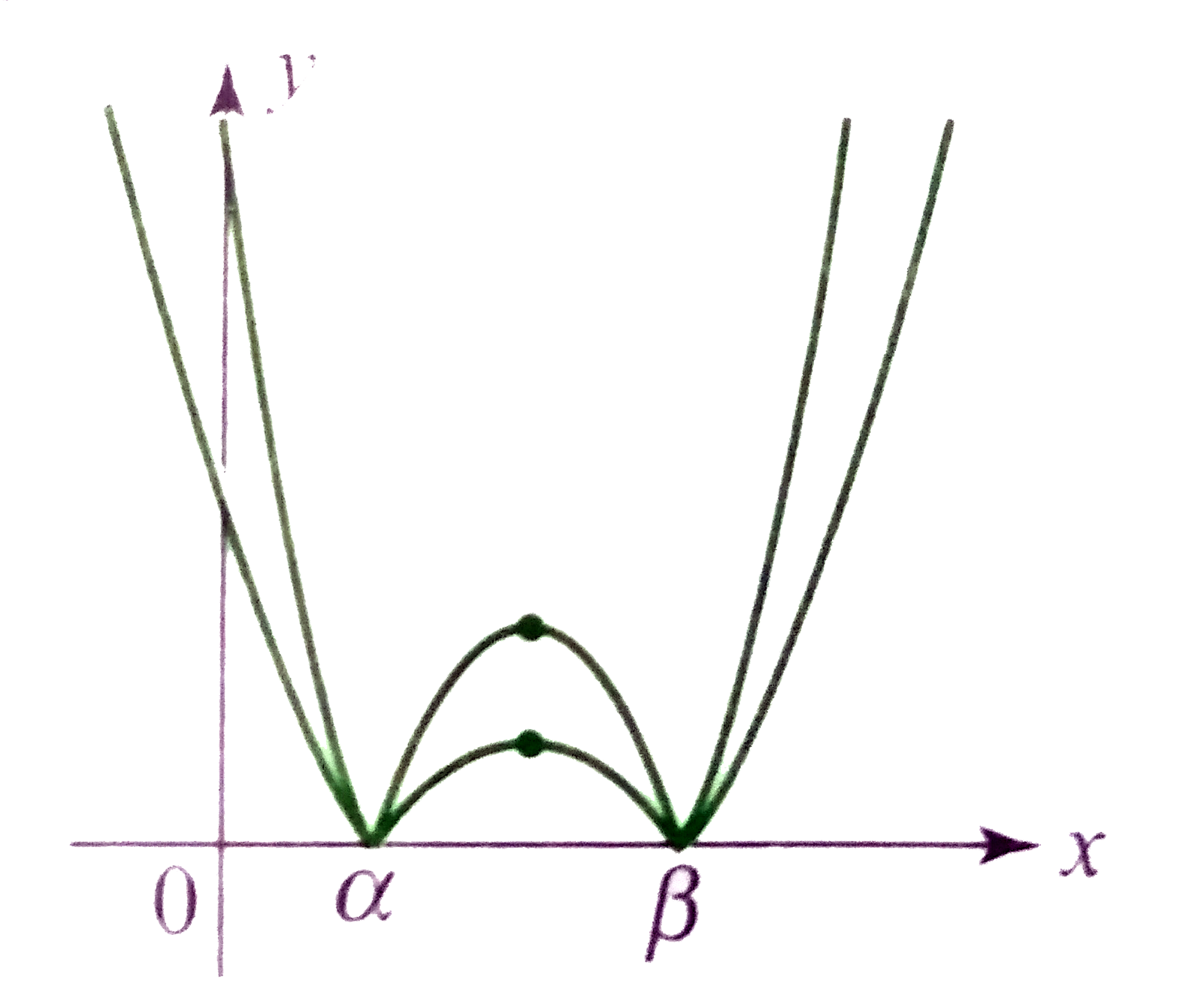
∣∣px2+qx+r∣∣≤∣∣Px2+Qx+R∣∣∀x∈R (1)
Form the graph we can see that this is possible only when both equations have same roots.
Thus, α and β are roots of Px2+Qx+R=0 and also of
px2+qx+r=0
So, from (1),
|p||x−α||x−β|≤|P||x−α||x−β|
⇒|p|≤|p|
Also ∣∣∣4pr−q24p∣∣∣≤∣∣∣4PR−Q24p∣∣∣
⇒|d|≤∣∣∣pP∣∣∣|D|
⇒|d|≤|D| (∵|p|≤|P|)
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - MATRIX MATCH TYPE
6 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - NUMERICAL VALUE TYPE
43 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer Type
38 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
291 Videos
Similar Questions
Match the following for the equation x2+a|x|+1=0 where, a is a parameter.

View SolutionIf x=2+22/3+21/3 , then the value of x3−6x2+6x is
View SolutionIf c≠0 and the equation p2x=ax+c+bx−c has two equal roots, then p can be
View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
View SolutionIf (x+2) is a common factor of (px^(2)+qx+r) and (qx^(2)+px+r) then a p=q or p+q+r=0 b p=r or p+q+r=0 c) q=r or p+q+r=0 d p=q=-(1)/(2)r
View SolutionProve that pxq−r+qxr−p+rxp−q>p+q+r,wherep,q,r are distinct andx≠1.
View SolutionIf p,q,r>0 and p!=q!=r such that,f(x)=px^(2)+2qx+r,g(x)=qx^(2)+2rx+p,f(x)=0 and g(x)=0 has a common root.
View SolutionIf the equations px^(2)+qx+r=0 and rx^(2)+qx+p=0 have a negative common root then the value of (p-q+r)=
View SolutionThe roots of the equation (q−r)x2+(r−p)x+p−q=0 are (A) r−pq−r,1 (B) p−qq−r,1 (C) q−rp−q,1 (D) r−pp−q,1
View SolutionIf p,q,rεR and the quadratic equation px2+qx+r=0 has no real roots, then (A) p(p+q+r)>0 (B) (p+q+r)>0 (C) q(p+q+r)>0 (D) p+q+r>0
View SolutionShow that the equations px2+qx+r=0 and qx2+px+r=0 will have a common root if p+q+r=0 or, p=q=r.
View Solution|(0,p-q,p-r),(q-p,0,q-r),(r-p,r-q,0)|=
View SolutionIf px3+qx2+rx+s=0 is a R.E .of second type then
p=s,q=r
p=-s,q=-r
p=s,q=-r
p=-s ,q=r
View SolutionIf (x+2) is a common factor of (px2+qx+r) and (qx2+px+r) then (a) p=q or p+q+r=0 (b)p=r or p+q+r=0 (c) q=r or p+q+r=0 (d)p=q=−12r
View Solutionरेखीय (p−q)x+(q−r)y+(r−p)=0
(q−r)x+(r−p)y+(p−q)=0
व (r−p)x+(p−q)y+(q−r)=0 है
View Solution
