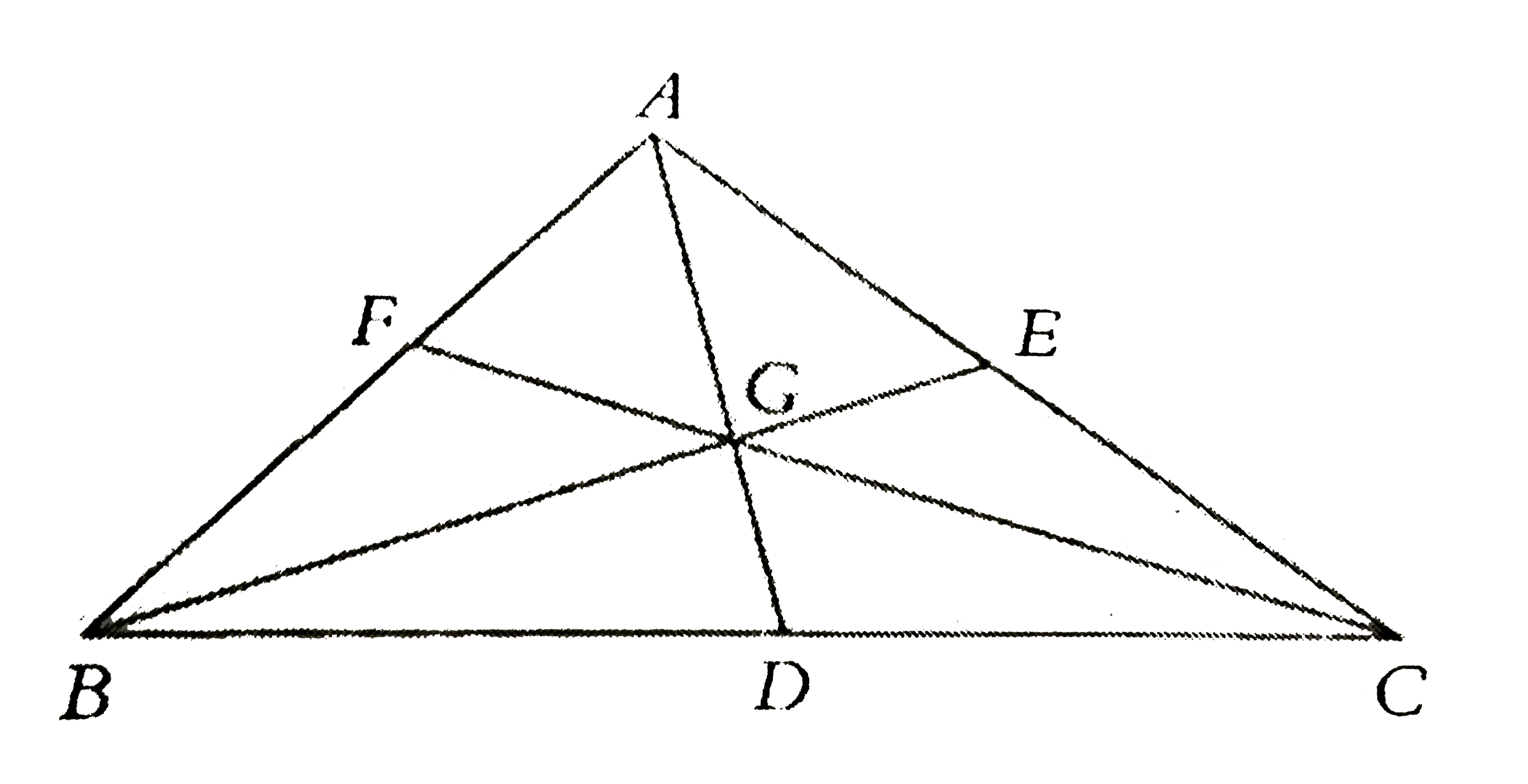
Let ABC be an acute- angled triangle and AD, BE, and CF be its medians, where E and F are at (3,4) and (1,2) respectively. The centroid of .
The coordinates of point D is ____________Solution in Bengali
The correct Answer is:C
Height of altitude from
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Matrix match type
4 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Numerical value
12 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Multiple correct
13 Videos
- COORDINATE SYSTEMBOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Consider the lines represented by equation (x2+xy−x)×(x−y)=0 forming a triangle. Then match the following lists:

View SolutionLine AB passes through point (2,3) and intersects the positive x and y-axes at A(a,0) and B(0,b) respectively. If the area of ΔAOB is 11. then the value of 4b2+9a2 is
View SolutionIf (-6,-4), (3,5),(-2,1) are the vertices of a parallelogram, then remaining vertex cannot be
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionLet ABC be an acute- angled triangle and AD, BE, and CF be its medians, where E and F are at (3,4) and (1,2) respectively. The centroid of ΔABC ,G(3,2).
The coordinates of D are
View SolutionLet ABC be an acute- angled triangle and AD, BE, and CF be its medians, where E and F are at (3,4) and (1,2) respectively. The centroid of ΔABC G(3,2).
The height of the altitude drawn from point A is (in units)
View SolutionAD, BE and CF are the medians of triangle ABC whose centroid is G. If the points A, F, G and E are concyclic, then prove that 2a2=b2+c2
View SolutionIn the given ΔABC,¯¯¯¯¯¯AD,¯¯¯¯¯¯BE and ¯¯¯¯¯¯CF are the medians. G is centroid. What is the ratio of the area of ΔBGD and ΔGCE?
View SolutionIf AD,BE and CF are the altitudes of a triangle ABC whose vertex A is the point (−4,5). The coordinates of the points E and F are (4,1) and (−1,−4) respectively, then equation of BC is
View SolutionLet D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
View SolutionLet ABC be an acute- angled triangle and AD, BE, and CF be its medians, where E and F are the points E(3,4) and F(1,2) respectively. The centroid of ΔABC ,G(3,2). equation of side AB is
View SolutionThe three medians AD, BE and CF of ΔABC intersect at point G. If the area of ΔABC is 60 sq.cm. then the area of the quadrilateral BDGF is :
View SolutionLet ABC be an acute- angled triangle and AD, BE, and CF be its medians, where E and F are at (3,4) and (1,2) respectively. The centroid of ΔABC G(3,2).
The coordinates of point D is ____________
View SolutionAD, BE and CF are the medians of triangle ABC whose centroid is G. If the points A, F, G and E are concyclic, then prove that 2a2=b2+c2
View SolutionIf AD,BE and CF are the altitudes of a triangle ABC whose vertex A is the point (−4,5). The coordinates of the points E and F are (4,1) and (−1,−4) respectively, then equation of BC is
View Solution
