Question

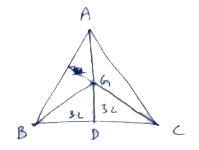
In a $\Delta ABC$, G is centroid and AD, BE, CF are medians. Find the area of quadrilateral BDGF, if the area of $\Delta ABC=72c{m}^2$

Options

A. 12
B. 16
C. 24
D. 8

Answer

24

Explanation

To find the area of quadrilateral BDGF in triangle ABC where G is the centroid and AD, BE, and CF are the medians, we can follow these steps:

1. Understand the Properties of Medians and Centroid:
- The medians of a triangle divide it into two triangles of equal area.
- The centroid (G) divides each median into two segments, one of which is twice the length of the other. Specifically, if D is the midpoint of BC, then the area of triangle ABD is equal to the area of triangle ADC.

2. Calculate the Area of Triangles Formed by the Medians:
- The area of triangle ABC is given as 72 cm².
- Since the medians divide triangle ABC into six smaller triangles of equal area, the area of each of these triangles is:
\( \text{Area of each triangle} = \frac{\text{Area of } \triangle ABC}{6} = \frac{72}{6} = 12 \text{ cm}^2 \)

3. Identify the Areas of Triangles BDG and BGF:
- The area of triangle BDG is one of these smaller triangles, so:
\( \text{Area of } \triangle BDG = 12 \text{ cm}^2 \)
- Similarly, the area of triangle BGF is also one of these smaller triangles, so:
\( \text{Area of } \triangle BGF = 12 \text{ cm}^2 \)

4. Calculate the Area of Quadrilateral BDGF:
- The area of quadrilateral BDGF is the sum of the areas of triangles BDG and BGF:
\( \text{Area of quadrilateral BDGF} = \text{Area of } \triangle BDG + \text{Area of } \triangle BGF = 12 \text{ cm}^2 + 12 \text{ cm}^2 = 24 \text{ cm}^2 \)

Final Answer:
The area of quadrilateral BDGF is 24 cm².