In a ΔABC,∠B=90∘, median AD and CF intersects at 'O' . Find the ratio of area of ΔAOCandBDOF.
The correct Answer is:1:1
To find the ratio of the areas of triangles AOC and BDOF in triangle ABC where angle B = 90°, follow these steps:
1. Draw Triangle ABC:
- Begin by sketching triangle ABC with angle B as a right angle. Label the vertices as A, B, and C, where B is at the right angle.
2. Identify the Medians:
- Draw the median AD from vertex A to the midpoint D of side BC.
- Draw the median CF from vertex C to the midpoint F of side AB.
- These medians intersect at point O.
3. Understanding the Properties of Medians:
- Recall that a median divides a triangle into two triangles of equal area. Therefore, median AD divides triangle ABC into two triangles: ABD and ACD, which have equal areas.
4. Determine Areas of Triangles:
- Since triangle ABC is divided into two equal areas by median AD, we can denote the area of triangle ABD as A and the area of triangle ACD as A. Thus, the total area of triangle ABC is 2A.
5. Area of Triangle AOC:
- The median CF divides triangle ACD into two smaller triangles: AOC and COF. Since CF is a median, the areas of triangles AOC and COF are equal. Therefore, the area of triangle AOC is A2.
6. Area of Quadrilateral BDOF:
- The area of quadrilateral BDOF can be calculated as the area of triangle ABC minus the area of triangle AOC.
- The area of triangle ABC is 2A and the area of triangle AOC is A2. Thus, the area of quadrilateral BDOF is:
Area of BDOF=Area of ABC−Area of AOC=2A−A2=4A2−A2=3A2
7. Finding the Ratio of Areas:
- Now, we can find the ratio of the area of triangle AOC to the area of quadrilateral BDOF:
Ratio=Area of AOCArea of BDOF=A23A2=13
Final Answer:
The ratio of the area of triangle AOC to the area of quadrilateral BDOF is 1:3.
- Begin by sketching triangle ABC with angle B as a right angle. Label the vertices as A, B, and C, where B is at the right angle.
- Draw the median AD from vertex A to the midpoint D of side BC.
- Draw the median CF from vertex C to the midpoint F of side AB.
- These medians intersect at point O.
- Recall that a median divides a triangle into two triangles of equal area. Therefore, median AD divides triangle ABC into two triangles: ABD and ACD, which have equal areas.
- Since triangle ABC is divided into two equal areas by median AD, we can denote the area of triangle ABD as A and the area of triangle ACD as A. Thus, the total area of triangle ABC is 2A.
- The median CF divides triangle ACD into two smaller triangles: AOC and COF. Since CF is a median, the areas of triangles AOC and COF are equal. Therefore, the area of triangle AOC is A2.
- The area of quadrilateral BDOF can be calculated as the area of triangle ABC minus the area of triangle AOC.
- The area of triangle ABC is 2A and the area of triangle AOC is A2. Thus, the area of quadrilateral BDOF is:
Area of BDOF=Area of ABC−Area of AOC=2A−A2=4A2−A2=3A2
- Now, we can find the ratio of the area of triangle AOC to the area of quadrilateral BDOF:
Ratio=Area of AOCArea of BDOF=A23A2=13
The ratio of the area of triangle AOC to the area of quadrilateral BDOF is 1:3.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a ΔABC,∠B=90∘, BN is perpendicular to AC. AB=6,AC=10. Find the ratio ANNC .
A916B43C169D34
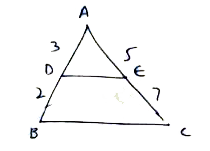
Find the ratio of area of ΔADE to Δ ABC
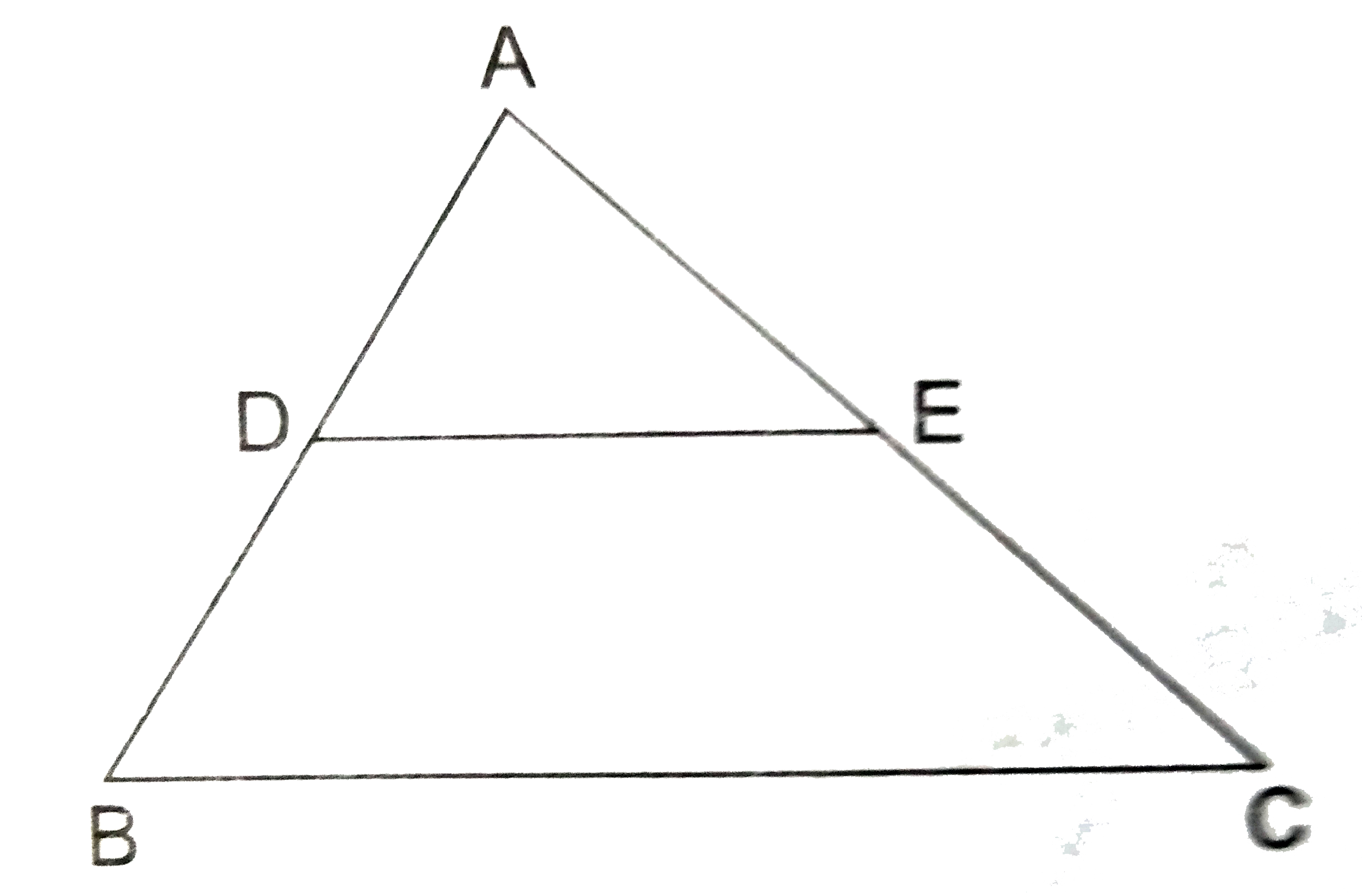
View SolutionABC is a triangle median CD and BE intersects at point O then find the ratio of area (ΔODE):(ΔABC).
View SolutionIn a ΔABC median BE and CF intersect at O ratio of area of OFEABC = ?
View SolutionIn ΔABC,DandE are the midpoint of AB and AC respectively. Find the ratio of the areas of ΔADEandΔABC.
View SolutionIn a ΔABC (right angled at B) , median BD of length l divides angle B in the ratio of 2:1 . Find area of ΔABC .
View SolutionIn a ΔABC,∠A=90∘,∠B=30∘ find the ratio of sides .
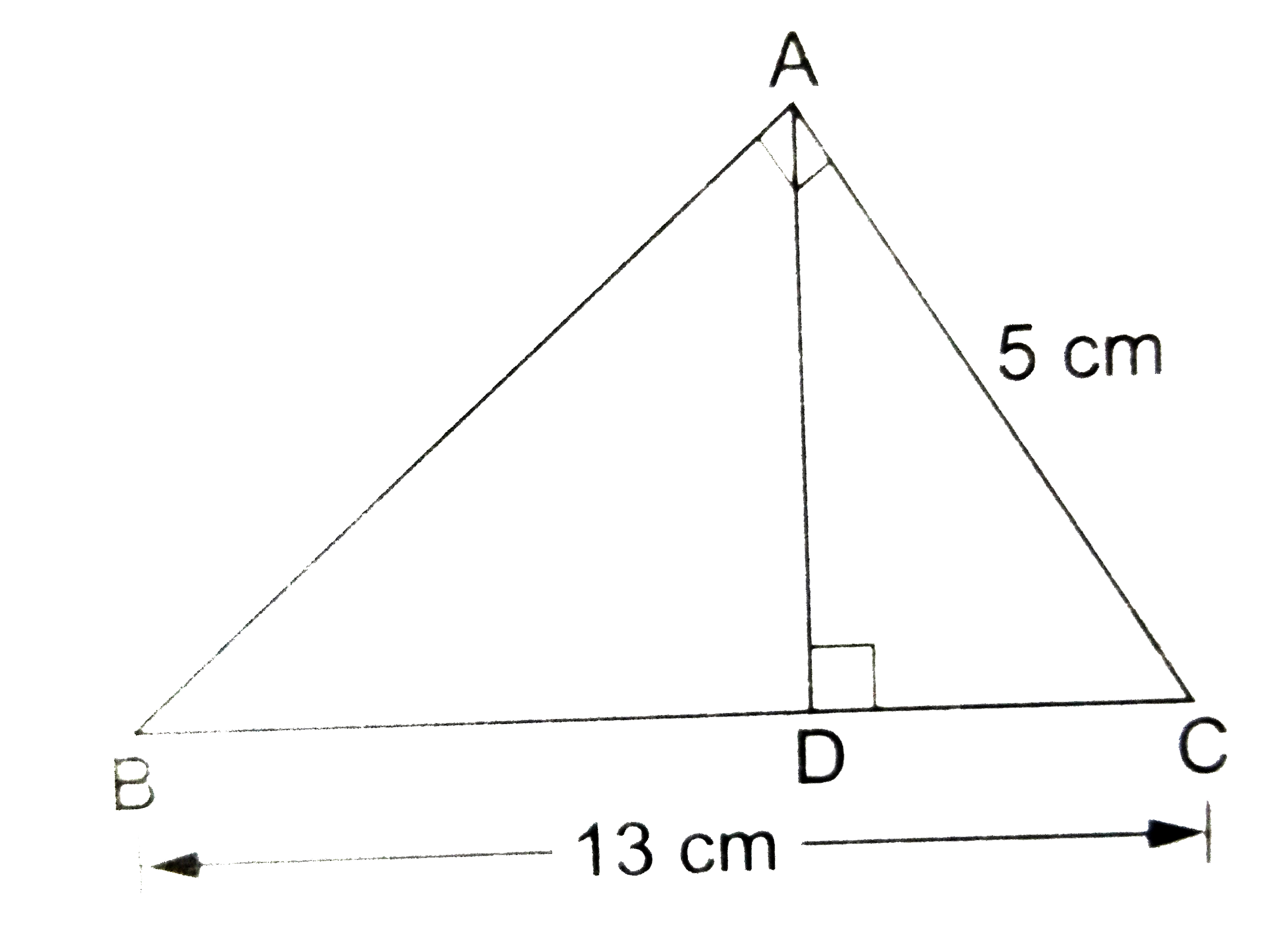
View SolutionΔABC is right-angled at A and AD⊥BC. If BC=13cmandAC=5cm, find the ratio of areas of ΔABCandΔADC.
View Solution
