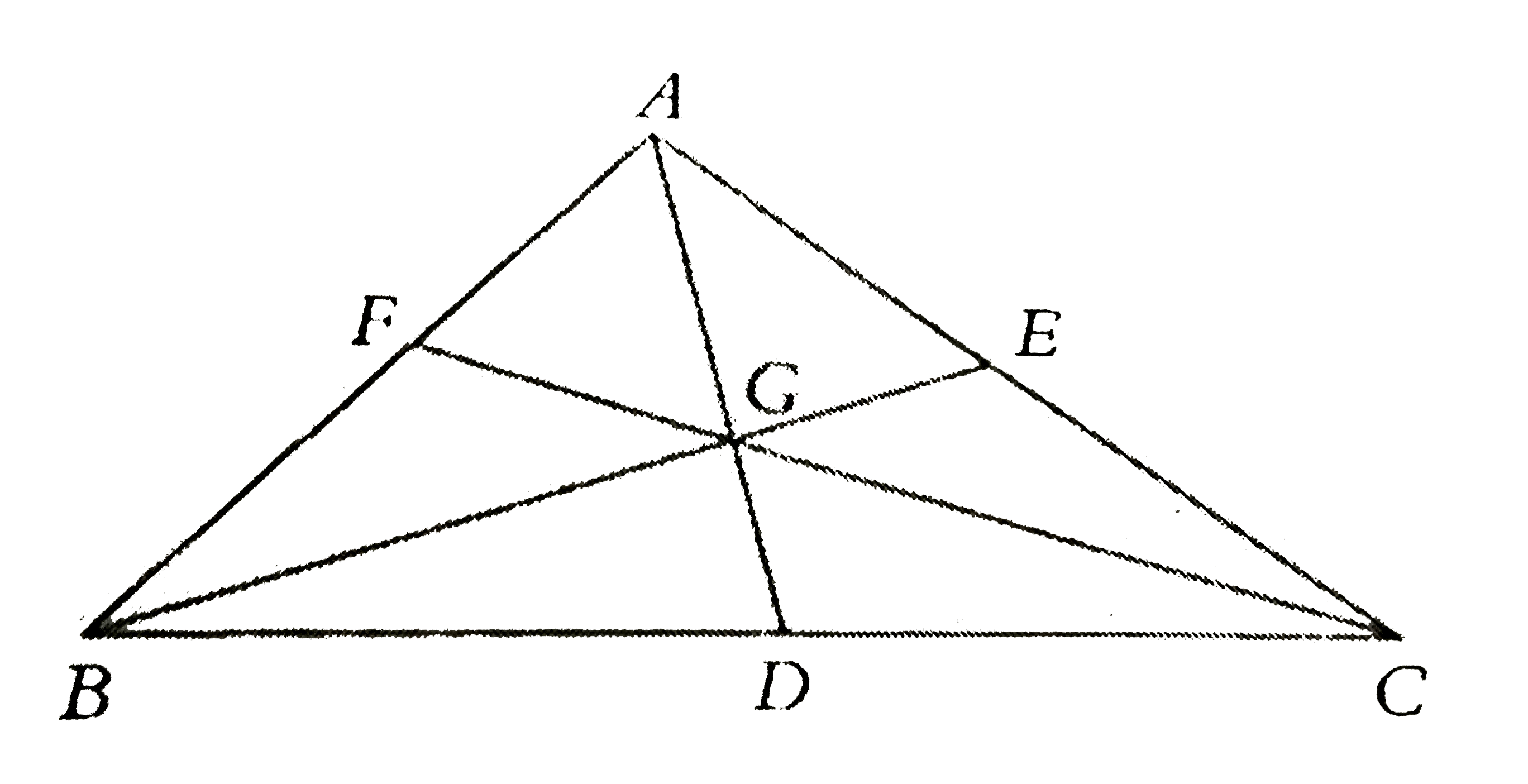
In the given $Δ A B C, ¯ ¯¯¯¯ ¯ A D, ¯ ¯¯¯¯ ¯ B E$ and $¯ ¯¯¯¯ ¯ C F$ are the medians. G is centroid. What is the ratio of the area of $Δ B G D$ and $Δ G C E$ ?

Video Solution

Text Solution

Verified by Experts

The three medians divide the triangle into six triangles of equal area. Hence, the ratio of the area of $Δ B G D$ to that of $Δ G C E$ is $1 : 1$

|

Updated on:21/07/2023

Class 8 MATHS PRACTICAL GEOMETRY

Topper's Solved these Questions

BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - very short answer type question
25videos
GEOMETRY
BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Short Answer Type Questions 31
9videos
GEOMETRY
BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FormulaeEXERCISE - Level 3
7videos
Formulae
BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)
7videos
INDICES

Similar Questions

Knowledge Check

Question 1 - Select One
In a $Δ A B C, A D, B E$ and CF are three medians. The perimeter of $Δ A B C$ is always.
Aequal to $(¯ ¯¯¯¯ ¯ A B + ¯ ¯¯¯¯ ¯ B E + ¯ ¯¯¯¯ ¯ C F)$
Bgreater than $(¯ ¯¯¯¯ ¯ A D + ¯ ¯¯¯¯ ¯ B E + ¯ ¯¯¯¯ ¯ C F)$
Cless than $(¯ ¯¯¯¯ ¯ A D + ¯ ¯¯¯¯ ¯ B E + ¯ ¯¯¯¯ ¯ C F)$
DNone of these
Question 2 - Select One
If G is the centroid of $Δ$ ABC, then $¯ ¯¯¯¯ ¯ C A + ¯ ¯¯¯¯ ¯ C B$ =
A3 $¯ ¯¯¯¯ ¯ G C$
B3 $¯ ¯¯¯¯ ¯ C G$
C3 $¯ ¯¯¯¯ ¯ A B$
D3 $¯ ¯¯¯¯ ¯ G A$

PEARSON IIT JEE FOUNDATION-GEOMETRY -CONCEPT APPLICATION (Level 1)

Home
Ask Doubt
Profile