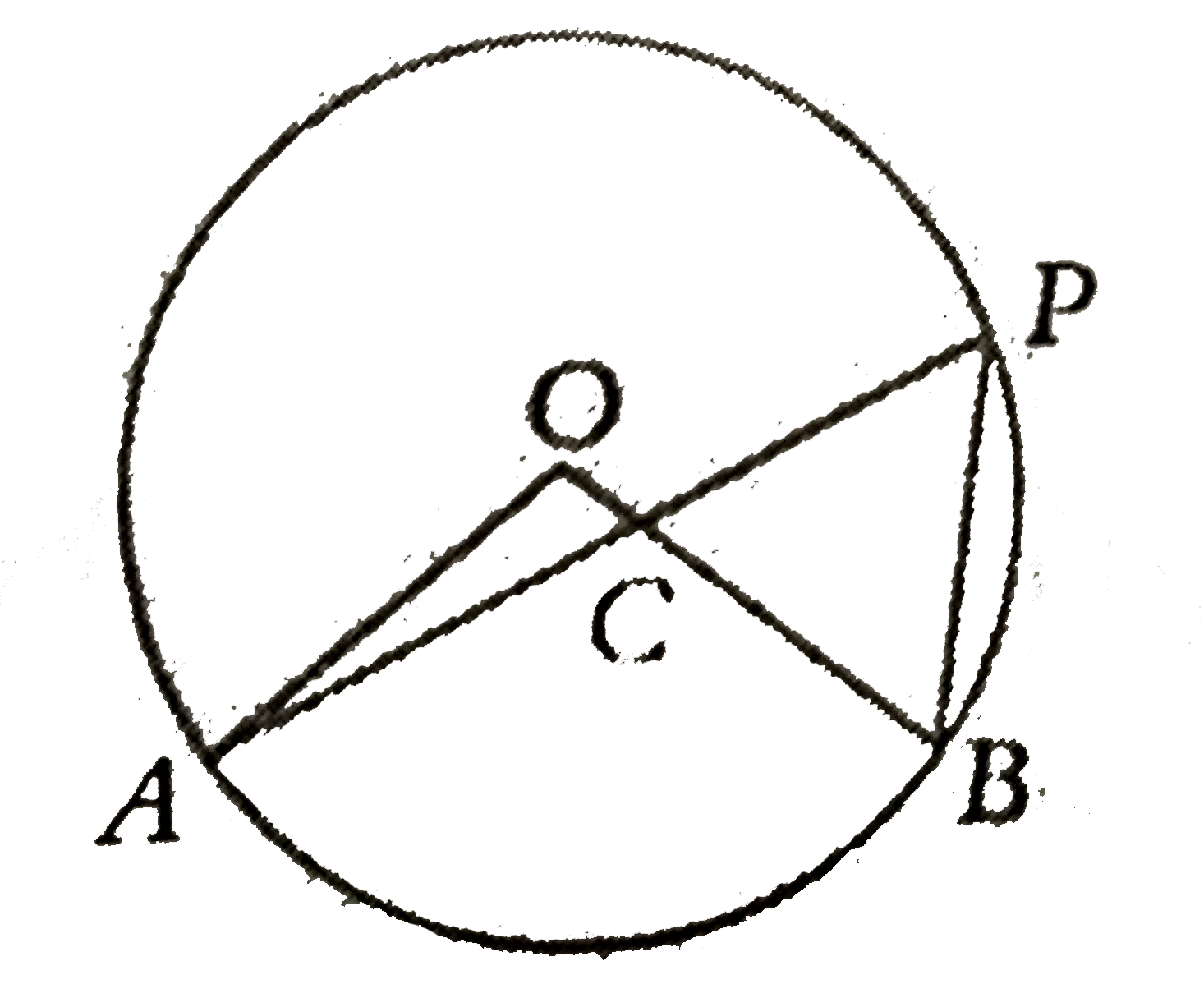
In the above figure (not to scale), O is the centre of the circle. and are two chords. C is the point of intersection of and . If and , then
The correct Answer is:B
Step by step video, text & image solution for In the above figure (not to scale), O is the centre of the circle. bar(AP) and bar(BP) are two chords. C is the point of intersection of bar(AP) and bar(OB). If /_ OAC= 30^(@) and /_ PBC =80^(@), then /_ AOB= by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - TEST YOUR CONCEPTS (ESSAY TYPE QUESTIONS)
5 Videos
- FormulaeBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FormulaeEXERCISE - Level 3
7 Videos
- INDICESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)
7 Videos
Similar Questions
Knowledge Check

In the above figure (not to scale), O is the centre of the circle. ¯¯¯¯¯¯AP and ¯¯¯¯¯¯BP are two chords. C is the point of intersection of ¯¯¯¯¯¯AP and ¯¯¯¯¯¯OB. If ∠OAC=30∘ and ∠PBC=80∘, then ∠AOB=A110∘B100∘C30∘D120∘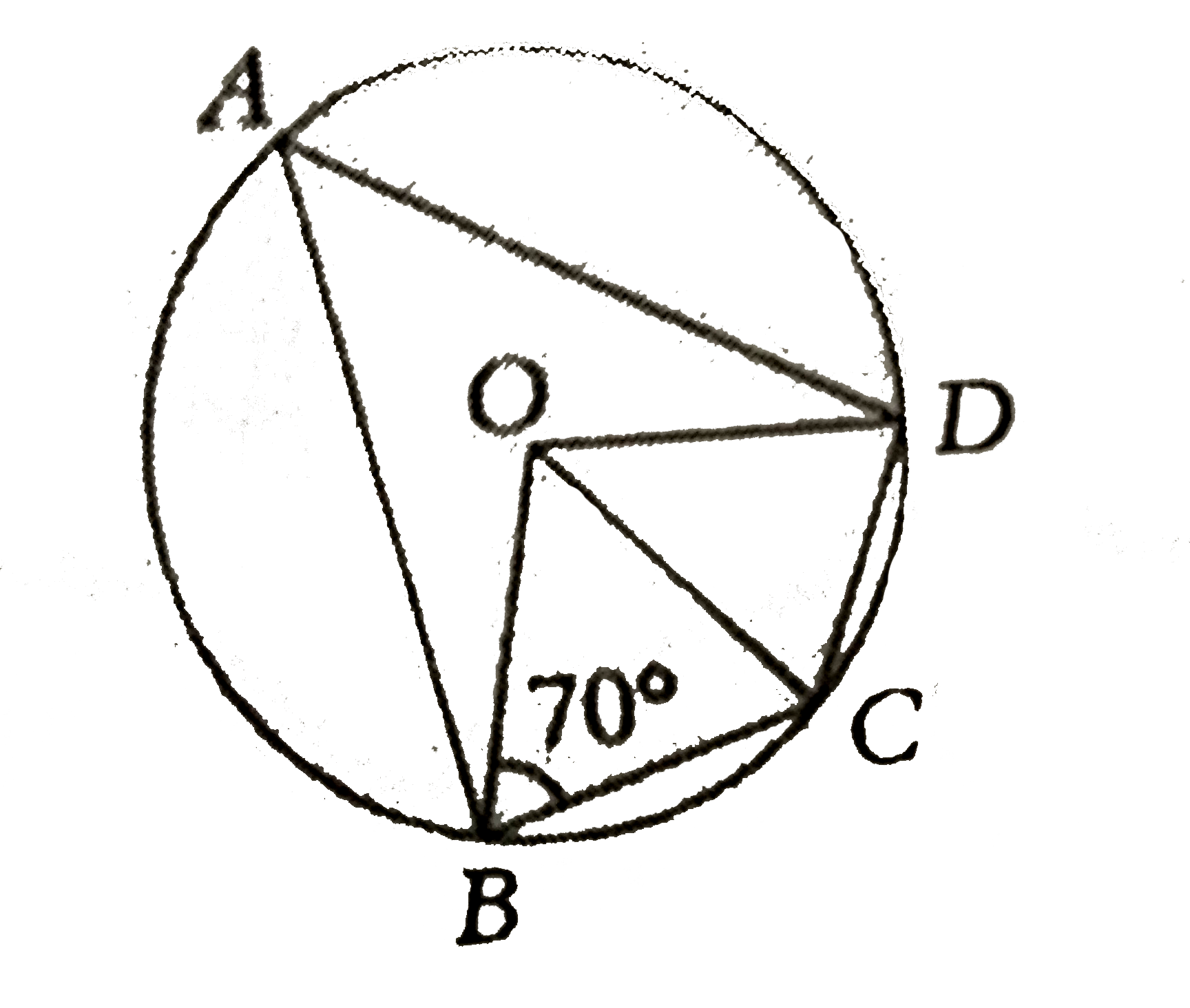
In the above figure (not to scale), O is the centre of the circle. ¯¯¯¯¯¯BC and ¯¯¯¯¯¯CD are equal chords. If ∠OBC=70∘ , then find ∠BAD.A40∘B60∘C55∘D45∘
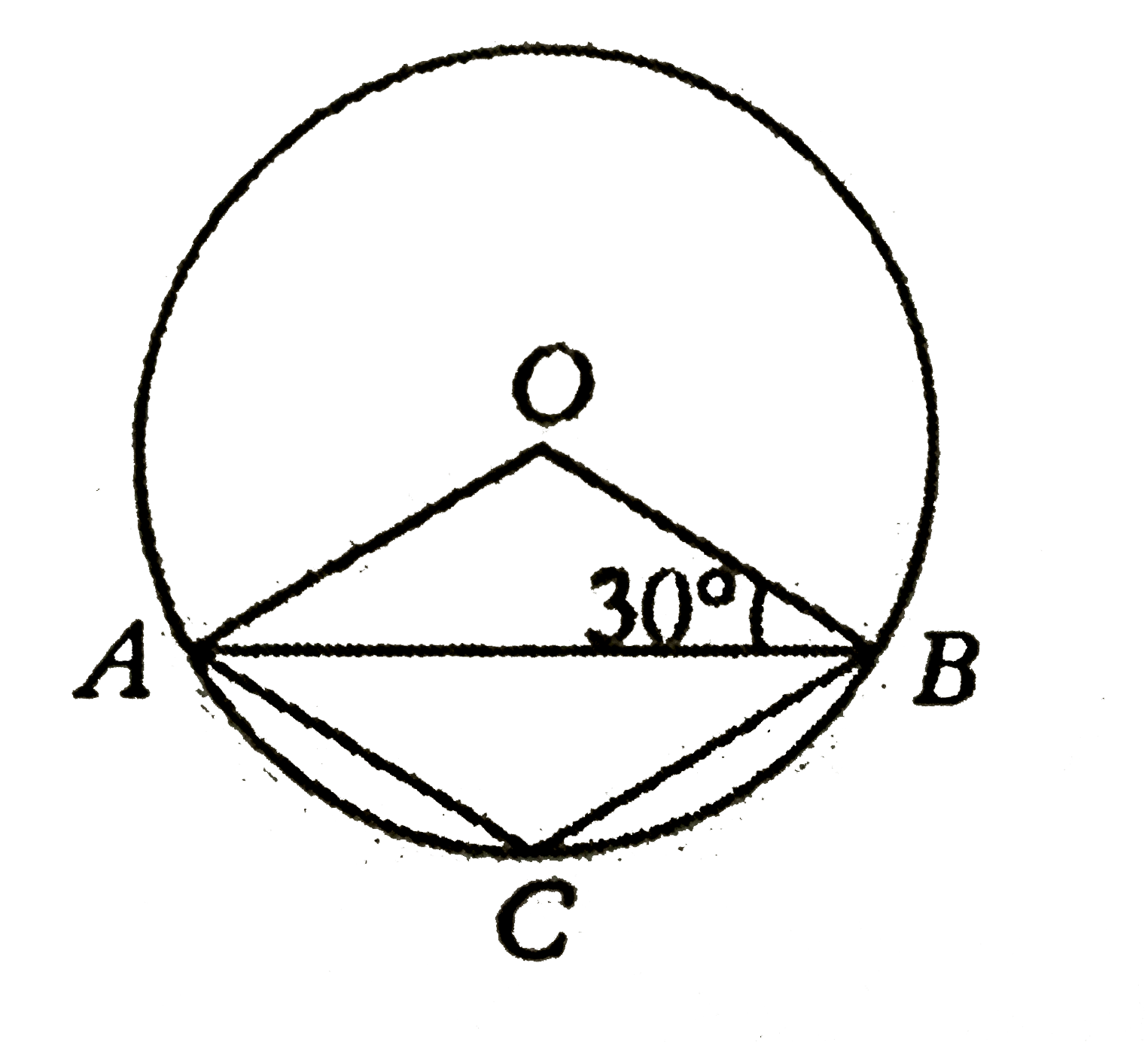
In the figure (not to scale ), O is the centre of the circle and ∠OBA=30∘. Find ∠ACB
View SolutionThe position vectors of the points A,B with respect to O are ¯a and ¯b and c is mid point of line segment ¯¯¯¯¯¯AB then ¯¯¯¯¯¯OC=
View SolutionIn the given figure, AB and CD are two equal chords. If O is the centre of the circle , ∠AOB=120∘, then find ∠OCD.
View Solution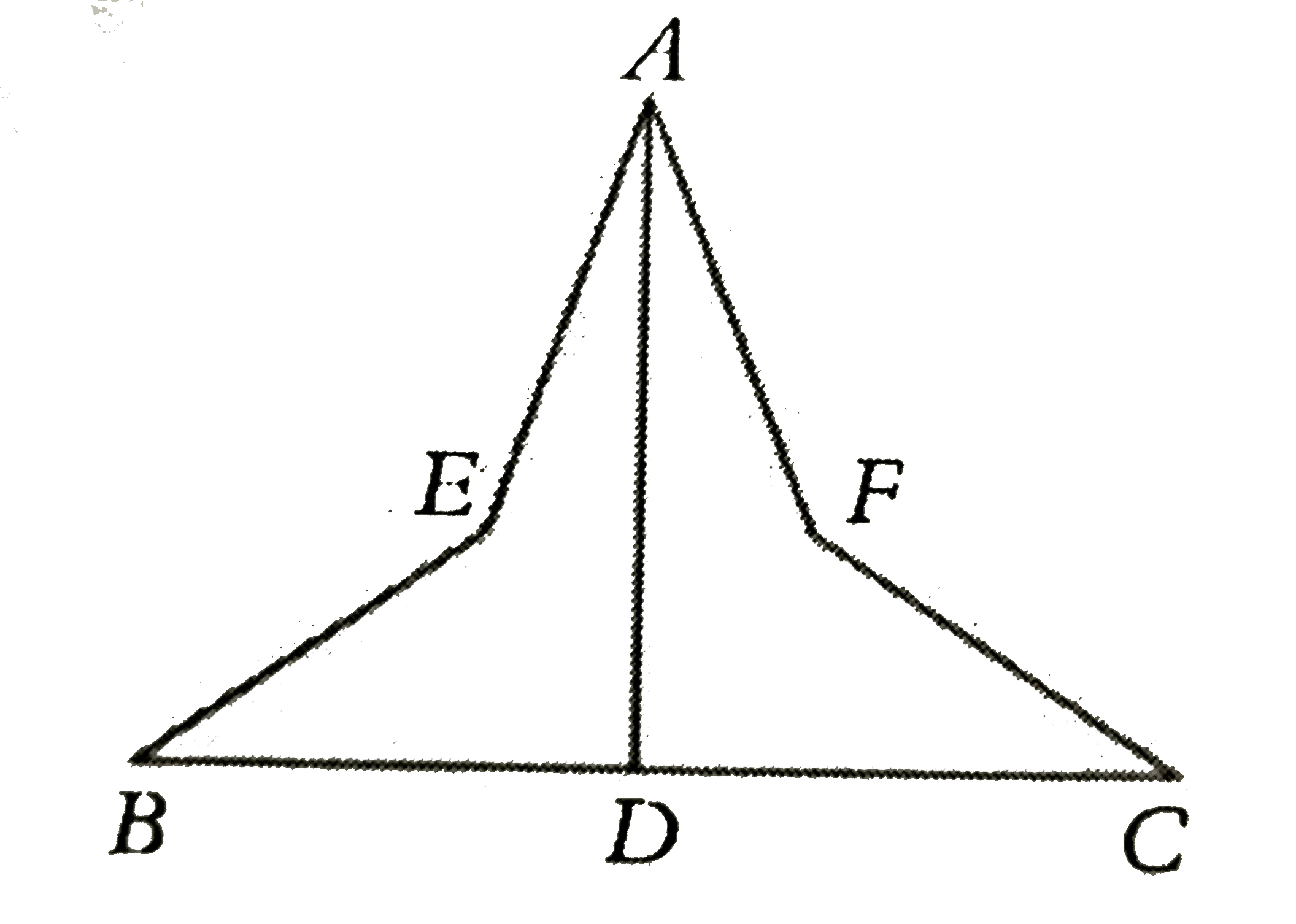
In the figuare above ( not to scale), ¯¯¯¯¯¯AD is the angle bisector of ∠EAF,∠AFC=110∘ and ∠DCF=20∘. If ∠DAF=30∘ and ∠EBD=10∘, then ∠AEB=
View Solution
In the above figure, ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯DE and ACE is a straight line . I f ∠ABC=30∘ and ∠CDE=20∘, then find ∠BCD.
View SolutionIn the following figure, O is the centre of the circle and ∠AMB=120∘ , Find the angle between the two tangents AP and BP.

View Solution

