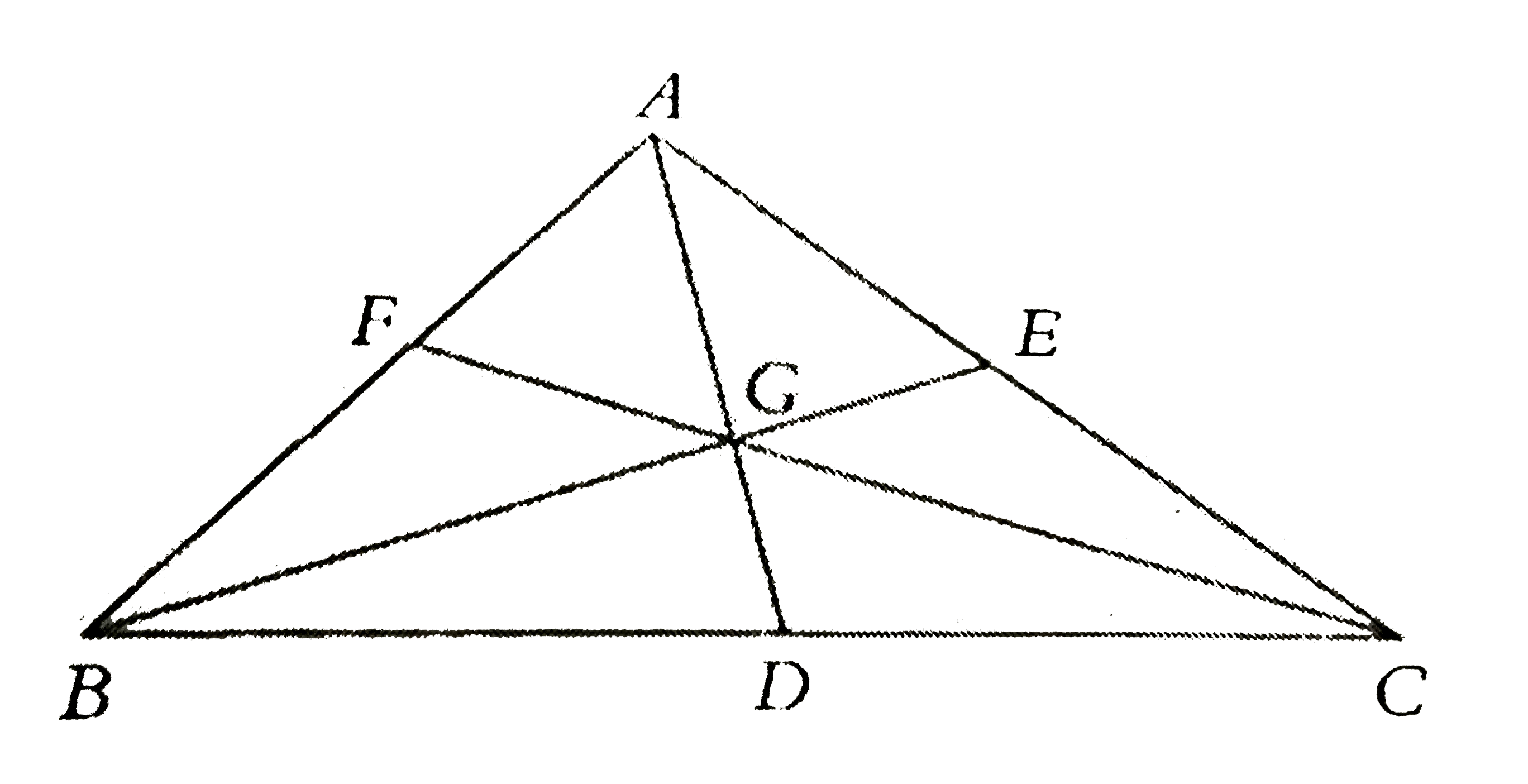
AD, BE and CF are the medians of triangle ABC whose centroid is G. If the points A, F, G and E are concyclic, then prove that 2a2=b2+c2Solution in Tamil
Points A, F, G and E are concylic,

⇒BG.BE=BF.BA
⇒23(BE)2=12c2
⇒23×14(2a2+2c2−b2)=12c2 (Using Apollonius Theorem)
⇒2a2=b2+c2
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.10
8 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.11
4 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.8
7 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBOOK - CENGAGECHAPTER - PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEEXERCISE - Question Bank
15 Videos
Similar Questions
In ΔABC, if r1<r2<r3, then find the order of lengths of the sides
View SolutionRegular pentagons are inscribed in two circles of radius 5and 2 units respectively. The ratio of their areas is
View SolutionIf the incircle of the triangle ABC passes through its circumcenter, then find the value of 4sin.A2sin.B2sin.C2
View SolutionIt is given that in a group of 4 students, the probability of 2 students not having the same birthday is 0.893. What is the probability that the 2 students have the same birthday?
View SolutionThe area of a right triangle is 6864 sq. units. If the ratio of its legs is 143:24, then the value of r is ______
View SolutionAD BE and CF are the medians of a Delta ABC .Prove that 2(AD+BE+CF)<3(AB+BC+CA)<4(AD+BE+CF)
View SolutionLet ABC be an acute- angled triangle and AD, BE, and CF be its medians, where E and F are at (3,4) and (1,2) respectively. The centroid of ΔABC G(3,2).
The height of the altitude drawn from point A is (in units)
View SolutionAD, BE and CF are the medians of triangle ABC whose centroid is G. If the points A, F, G and E are concyclic, then prove that 2a2=b2+c2
View SolutionIn the given ΔABC,¯¯¯¯¯¯AD,¯¯¯¯¯¯BE and ¯¯¯¯¯¯CF are the medians. G is centroid. What is the ratio of the area of ΔBGD and ΔGCE?
View SolutionLet ABC be an acute- angled triangle and AD, BE, and CF be its medians, where E and F are the points E(3,4) and F(1,2) respectively. The centroid of ΔABC ,G(3,2). equation of side AB is
View SolutionA=(1,3,-2) is a vertex of triangle ABC whose centroid is G=(-1,4,2) then length of median through A is
View SolutionThe three medians AD, BE and CF of ΔABC intersect at point G. If the area of ΔABC is 60 sq.cm. then the area of the quadrilateral BDGF is :
View SolutionLet ABC be an acute- angled triangle and AD, BE, and CF be its medians, where E and F are at (3,4) and (1,2) respectively. The centroid of ΔABC G(3,2).
The coordinates of point D is ____________
View SolutionAD, BE and CF are the medians of triangle ABC whose centroid is G. If the points A, F, G and E are concyclic, then prove that 2a2=b2+c2
View SolutionIn a ΔABC, G is centroid and AD, BE, CF are medians. Find the area of quadrilateral BDGF, if the area of ΔABC=72cm2
View Solution
